filmov
tv
Angle Chasing Geometry Problem | Math Olympiad

Показать описание
Angle Chasing Geometry Problem | Math Olympiad
MY OTHER CHANNELS
••••••••••••••••••••••••••••••••
--------------------------------------------------------------------------------
Join the channel to become a member
angle chasing
geometry problems
angle chasing olympiad problems
geometry
maths olympiad
iran geometry olympiad
math olympiad geometry problems
math olympiad
angle chasing problems
maths olympiad geometry questions
olympiad problems on geometry
geometry problem
math olympiad problems
math olympiad geometry
how to solve this tricky geometry problem quickly
problems on geometry
asian math olympiad
olympiad
what is angle chasing
olympiad mathematics
MY OTHER CHANNELS
••••••••••••••••••••••••••••••••
--------------------------------------------------------------------------------
Join the channel to become a member
angle chasing
geometry problems
angle chasing olympiad problems
geometry
maths olympiad
iran geometry olympiad
math olympiad geometry problems
math olympiad
angle chasing problems
maths olympiad geometry questions
olympiad problems on geometry
geometry problem
math olympiad problems
math olympiad geometry
how to solve this tricky geometry problem quickly
problems on geometry
asian math olympiad
olympiad
what is angle chasing
olympiad mathematics
Angle Chasing Problem - Moscow 1952 | A Nice Geometry Challenge
Find the angle X | Angle Chasing Geometry Problem | Important Geometry Skills Explained
How To Solve For The Angle - Viral Math Challenge
A Very Nice Angle Chasing Geometry Problem | Math Olympiad
Angle Chasing Problem | Find the angle θ | Geometry | Ukrainian Junior Maths Olympiad
Angle Chasing Geometry Problem | Math Olympiad
Chinese Junior Math Olympiad Problem | Angle Chasing Geometry Problem
Geometry Problem | Finding the Missing Angle | SAT Prep | Math Problem
MOST TRICKY || ANGLE CHASING PROBLEM || geometry
Geometry | Angle Chasing | Easy Problem | Two Equilateral Triangle | Mathematical Olympiads
An example of angle chasing
Angle Chasing I A nice geometry problem for exams OLYMPIAD I SAT I MCAT I Xth I GRE I Pre-Math I
Geometry Angle chasing problem
Missing Angles Geometry Problem | Tricky Math Question | JusticeTheTutor #maths #math #shorts
A Classically Hard Geometry Problem
Can You Find Angle X? | Geometry Challenge!
9 4-Step Angle-Chasing
Geometry Tutorial #2 -Angle Chasing (Practice)
Can you find the angle | Angle Chasing | Geometry | Quantitative Aptitude
The missing angle - geometry puzzle!
A magical reflection| Angle Chasing| The Ultimate Geo Course
Angle Chasing Observation | Geometry | Mathematics Olympiad IOQM 2023 | Abhay Sir | VOS
Angle Chasing - Mastering AMC 10/12
Geometry | Lecture - 3 | Problems on Angle Chasing | Olympiads | Abhilash Verma
Комментарии
 0:09:25
0:09:25
 0:08:55
0:08:55
 0:04:06
0:04:06
 0:09:41
0:09:41
 0:06:35
0:06:35
 0:08:28
0:08:28
 0:04:39
0:04:39
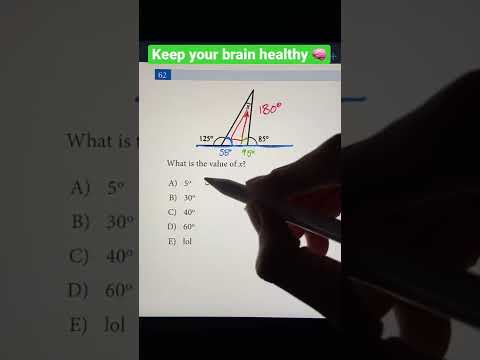 0:00:44
0:00:44
 0:02:26
0:02:26
 0:02:48
0:02:48
 0:05:16
0:05:16
 0:06:20
0:06:20
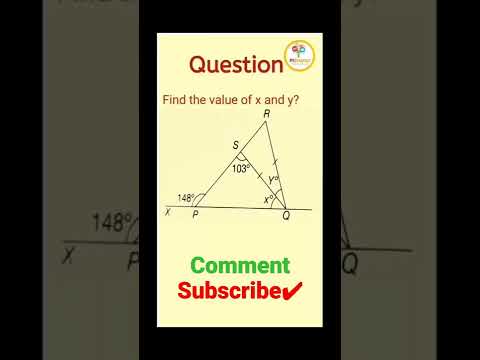 0:00:02
0:00:02
 0:00:37
0:00:37
 0:05:10
0:05:10
 0:08:44
0:08:44
 0:04:00
0:04:00
 0:54:05
0:54:05
 0:04:35
0:04:35
 0:00:37
0:00:37
 0:11:47
0:11:47
 1:26:11
1:26:11
 0:20:48
0:20:48
 0:38:30
0:38:30