filmov
tv
Angle Chasing Problem | Find the angle θ | Geometry | Ukrainian Junior Maths Olympiad

Показать описание
Find the angle θ | Angle Chasing Problem | Geometry | Ukrainian Junior Maths Olympiad
Join this channel to get access to perks:
MEMBERS OF THIS CHANNEL
••••••••••••••••••••••••••••••••••••••••
Mr. Gnome
Sambasivam Sathyamoorthy
ஆத்தங்கரை சண்முகம்
Εκπαιδευτήρια Καντά
AR Knowledge
堤修一
Sidnei Medeiros Vicente
Mark Ludington
Saunak Swar
Join this channel to get access to perks:
MEMBERS OF THIS CHANNEL
••••••••••••••••••••••••••••••••••••••••
Mr. Gnome
Sambasivam Sathyamoorthy
ஆத்தங்கரை சண்முகம்
Εκπαιδευτήρια Καντά
AR Knowledge
堤修一
Sidnei Medeiros Vicente
Mark Ludington
Saunak Swar
Angle Chasing Problem | Find the angle θ | Geometry | Ukrainian Junior Maths Olympiad
Angle Chasing Problem - Moscow 1952 | A Nice Geometry Challenge
Find the angle X | Angle Chasing Geometry Problem | Important Geometry Skills Explained
AMC8 Course | Angle Chasing | Problem 1
Can you find the measure of angle OPQ..? | Interesting angle chasing problem.||Geometry.||Circle.||
A Very Nice Angle Chasing Geometry Problem | Math Olympiad
Find ∠CEB. Angle chasing problem.|| Square and Semicircle.|| Tangent.|| 90° || Alternate segment....
How To Solve For The Angle - Viral Math Challenge
Geometry Problem | Finding the Missing Angle | SAT Prep | Math Problem
Chinese Junior Math Olympiad Problem | Angle Chasing Geometry Problem
A magical reflection| Angle Chasing| The Ultimate Geo Course
Can you find the angle | Angle Chasing | Geometry | Quantitative Aptitude
An example of angle chasing
Geometry Angle chasing problem
Find ∠ BAC. || Angle Chasing.|| ∠BAE = ∠ADC.|| BE : EC = 2 : 1. || Triangles with common vertex....
Angle Chasing Geometry Problem | Math Olympiad
Angles in a Triangle - Angle Chasing
Can You Find Angle X? | Geometry Challenge!
MOST TRICKY || ANGLE CHASING PROBLEM || geometry
9 4-Step Angle-Chasing
Angle Chasing with Algebra, Tier 3
The missing angle - geometry puzzle!
Angle Chasing with folded paper
Geometry Tutorial #2 -Angle Chasing (Practice)
Комментарии
 0:06:35
0:06:35
 0:09:25
0:09:25
 0:08:55
0:08:55
 0:08:45
0:08:45
 0:07:34
0:07:34
 0:09:41
0:09:41
 0:06:40
0:06:40
 0:04:06
0:04:06
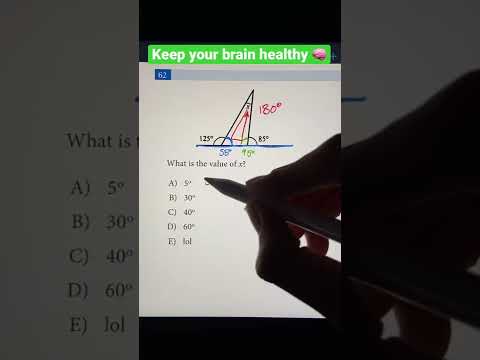 0:00:44
0:00:44
 0:04:39
0:04:39
 0:11:47
0:11:47
 0:04:35
0:04:35
 0:05:16
0:05:16
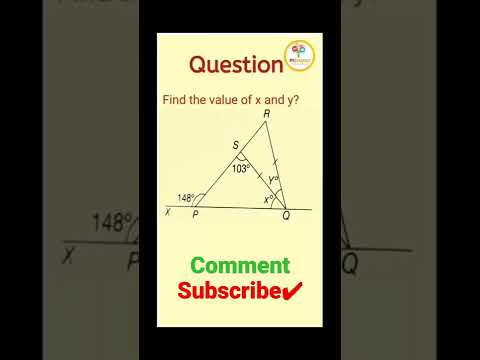 0:00:02
0:00:02
 0:06:18
0:06:18
 0:08:28
0:08:28
 0:06:37
0:06:37
 0:08:44
0:08:44
 0:02:26
0:02:26
 0:04:00
0:04:00
 0:15:01
0:15:01
 0:00:37
0:00:37
 0:07:04
0:07:04
 0:54:05
0:54:05