filmov
tv
A Nice Polynomial Equation | Cubic Formula?
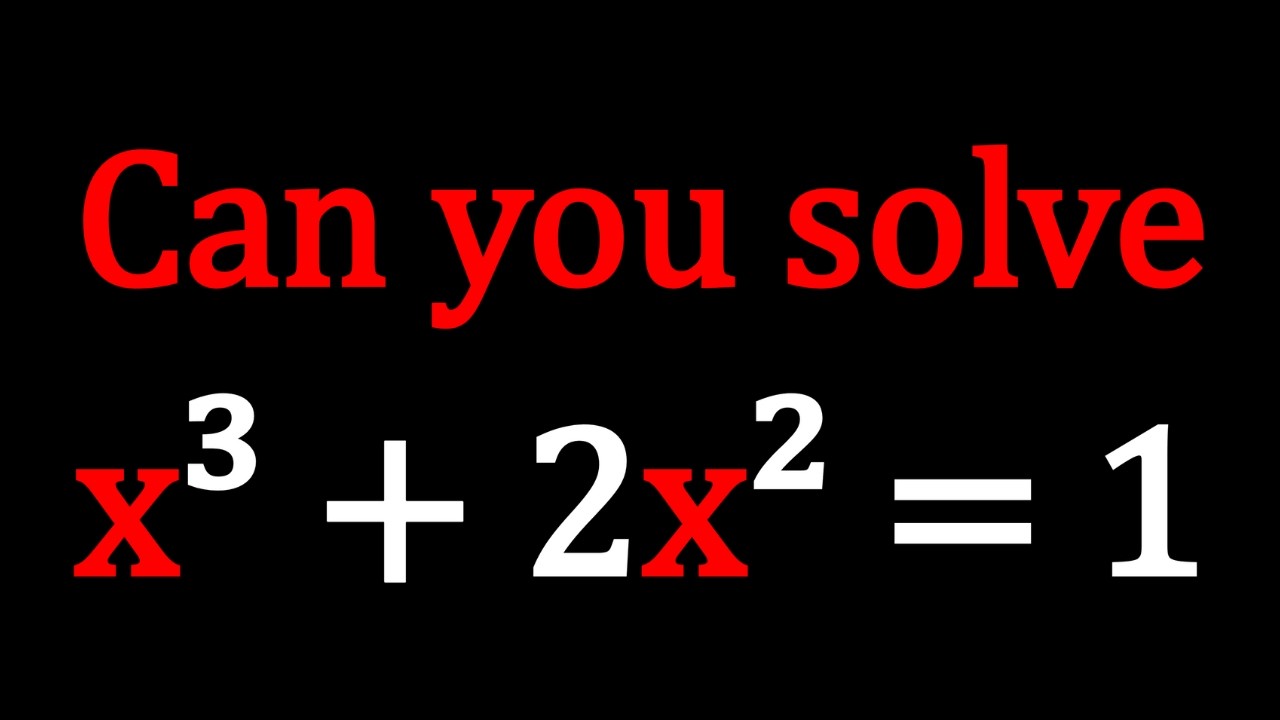
Показать описание
🤩 Hello everyone, I'm very excited to bring you a new channel (aplusbi)
Enjoy...and thank you for your support!!! 🧡🥰🎉🥳🧡
When you purchase something from here, I will make a small percentage of commission that helps me continue making videos for you.
If you are preparing for Math Competitions and Math Olympiads, then this is the page for you!
You can find ARML books and many others here. CHECK IT OUT!!! ❤️ ❤️ ❤️
If you need to post a picture of your solution or idea:
#radicals #radicalequations #algebra #calculus #differentialequations #polynomials #prealgebra #polynomialequations #numbertheory #diophantineequations #comparingnumbers #trigonometry #trigonometricequations #complexnumbers #math #mathcompetition #olympiad #matholympiad #mathematics #sybermath #aplusbi #shortsofsyber #iit #iitjee #iitjeepreparation #iitjeemaths #exponentialequations #exponents #exponential #exponent #systemsofequations #systems
#functionalequations #functions #function #maths #counting #sequencesandseries
#algebra #numbertheory #geometry #counting #mathcontests #mathcompetitions
via @YouTube @Apple @Desmos @NotabilityApp @googledocs @canva
PLAYLISTS 🎵 :
Enjoy...and thank you for your support!!! 🧡🥰🎉🥳🧡
When you purchase something from here, I will make a small percentage of commission that helps me continue making videos for you.
If you are preparing for Math Competitions and Math Olympiads, then this is the page for you!
You can find ARML books and many others here. CHECK IT OUT!!! ❤️ ❤️ ❤️
If you need to post a picture of your solution or idea:
#radicals #radicalequations #algebra #calculus #differentialequations #polynomials #prealgebra #polynomialequations #numbertheory #diophantineequations #comparingnumbers #trigonometry #trigonometricequations #complexnumbers #math #mathcompetition #olympiad #matholympiad #mathematics #sybermath #aplusbi #shortsofsyber #iit #iitjee #iitjeepreparation #iitjeemaths #exponentialequations #exponents #exponential #exponent #systemsofequations #systems
#functionalequations #functions #function #maths #counting #sequencesandseries
#algebra #numbertheory #geometry #counting #mathcontests #mathcompetitions
via @YouTube @Apple @Desmos @NotabilityApp @googledocs @canva
PLAYLISTS 🎵 :
Комментарии
 0:10:00
0:10:00
 0:05:53
0:05:53
 0:14:19
0:14:19
 0:08:35
0:08:35
 0:00:51
0:00:51
 0:08:40
0:08:40
 0:08:26
0:08:26
 0:09:27
0:09:27
 0:00:22
0:00:22
 0:09:03
0:09:03
 0:09:47
0:09:47
 0:09:27
0:09:27
 0:09:34
0:09:34
 0:08:19
0:08:19
 0:08:13
0:08:13
 0:09:53
0:09:53
 0:10:56
0:10:56
 0:09:32
0:09:32
 0:08:38
0:08:38
 0:10:56
0:10:56
 0:08:57
0:08:57
 0:12:02
0:12:02
 0:09:37
0:09:37
 0:10:45
0:10:45