Geometric Animation of Integrating e^(ix) from 0 to π

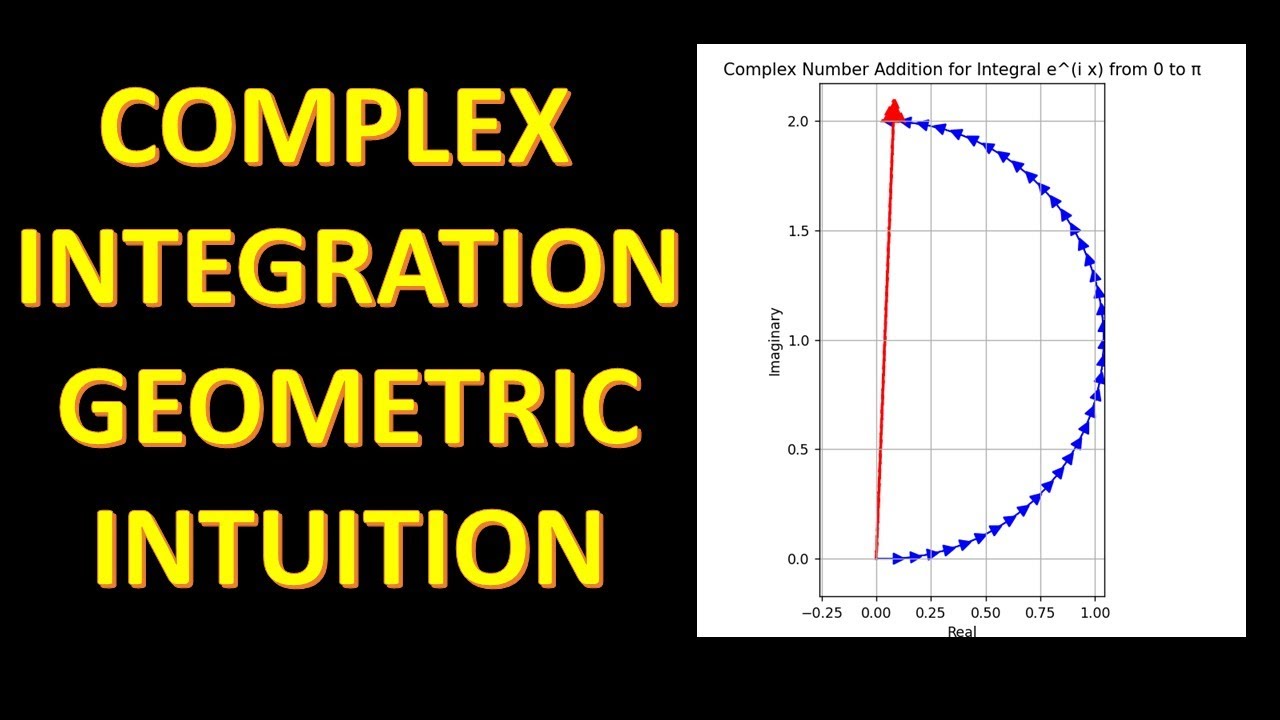
In this video, we demonstrate the process of visualizing the integration of complex numbers along the curve e^(ix) from 0 to π using arrows. This approach helps provide an intuitive understanding of complex number integration and how it relates to vector addition.

Complex number integration involves summing up the contributions of complex numbers along a curve in the complex plane. In our example, we consider the curve e^(ix) from 0 to π, where x is the real variable and i is the imaginary unit (i^2 = -1).

We start by dividing the interval [0, π] into 'n' equally spaced points. For each point, we calculate the corresponding complex number e^(ix), which lies on the unit circle in the complex plane. The magnitude of each complex number is scaled by the difference in angle between consecutive points (delta_theta), which represents the arc length along the unit circle.

To visualize the integration, we draw scaled arrows from the origin to each complex number in the complex plane. The arrow representing the complex number at a point x is the vector from the origin to the point e^(ix) scaled by delta_theta. The sum of these arrows represents the integral of e^(ix) from 0 to π.

As we animate the process of adding the scaled arrows, you can see how the vector sum approximates the integral. This visualization helps build intuition for complex number integration and provides a clear understanding of the relationship between complex numbers and vector addition in the complex plane.

Watch the video to see this fascinating process in action and gain a deeper understanding of complex number integration!

[skillick]

You could do a similar visualisation demonstrating the FTC still works.

[TheFireBrozTFB]

That is interesting, complex integration always seemed weird to me, though this idea clarifies it quite a bit. Cheers!