filmov
tv
What does area have to do with slope? | Chapter 9, Essence of calculus
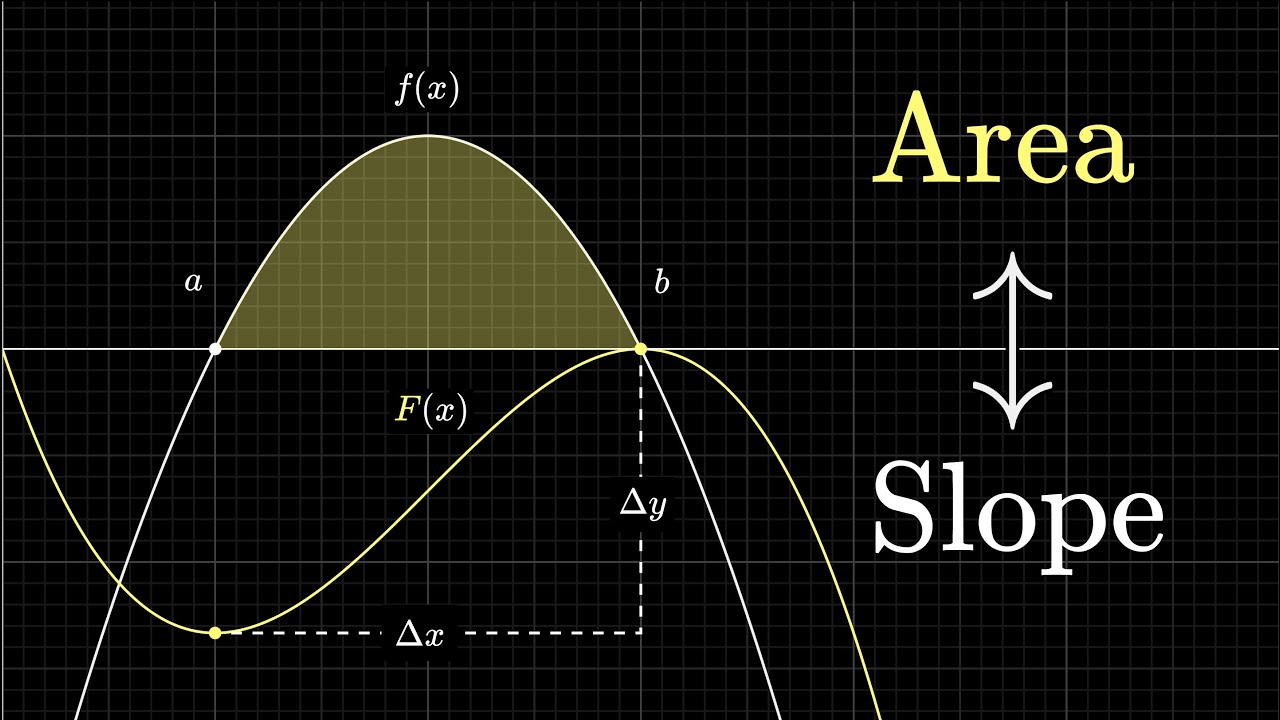
Показать описание
One view on why integrals and derivatives are inverses.
An equally valuable form of support is to simply share some of the videos.
Thanks to these viewers for their contributions to translations
Hebrew: Omer Tuchfeld
Vietnamese: ngvutuan2811
------------------
3blue1brown is a channel about animating math, in all senses of the word animate. And you know the drill with YouTube, if you want to stay posted about new videos, subscribe, and click the bell to receive notifications (if you're into that).
Various social media stuffs:
An equally valuable form of support is to simply share some of the videos.
Thanks to these viewers for their contributions to translations
Hebrew: Omer Tuchfeld
Vietnamese: ngvutuan2811
------------------
3blue1brown is a channel about animating math, in all senses of the word animate. And you know the drill with YouTube, if you want to stay posted about new videos, subscribe, and click the bell to receive notifications (if you're into that).
Various social media stuffs:
What does area have to do with slope? | Chapter 9, Essence of calculus
Calculus: Why does integrating a function give area under its curve?
What Does the Area Under a Growth Curve Mean? : Physics & Science Lessons
What does the second derivative have to do with area??
Does this red region have a name?? Let's find its area!
Does the Area of a Closed Shape Increase When the Perimeter Increases?
What does area even mean? - Week 11 - Lecture 6 - Mooculus
why does unit of area of shapes have square??? #mathematics #math #area #rectangle #basicshapes
Ann Arbor Area Golf, Life, & Fun - 2024 MGL TV
Does an infinite region have to have infinite area? -- Calculus II
The European Union Explained*
Does 'land area' assume a country is perfectly flat?
Surface Area of a Cone- why does it work?
Ukraine-Russia war: How long can Ukraine hold Kursk?
Why does integrating the function of a curve give you the area under the curve?
Area A in Phase 2 of the #123rdCantonFair——what does it have?
How well does your area perform?
Mensuration: The Area of a square. What does this mean? A drawing approach
Black Myth: Wukong - How to Unlock the Secret Area In Chapter 2
Why Does This Area Have So Much Gold#prospecting
Does Area 51 have anything to do with aliens?
At Home Learning - What Does Multiplication Have to Do with Area Math Grade 3
Why does DC's 202 area code have to go away?
Why does this secret area hide a boss?
Комментарии
 0:12:39
0:12:39
 0:09:36
0:09:36
 0:03:25
0:03:25
 0:18:24
0:18:24
 0:08:22
0:08:22
 0:01:31
0:01:31
 0:07:10
0:07:10
 0:00:43
0:00:43
 0:25:13
0:25:13
 0:46:15
0:46:15
 0:05:51
0:05:51
 0:17:51
0:17:51
 0:13:18
0:13:18
 0:03:44
0:03:44
 0:16:45
0:16:45
 0:00:35
0:00:35
 0:00:24
0:00:24
 0:10:34
0:10:34
 0:03:18
0:03:18
 0:11:27
0:11:27
 0:00:51
0:00:51
 0:10:43
0:10:43
 0:02:54
0:02:54
 0:01:59
0:01:59