filmov
tv
Solving the Exponential Equation x^x=2^{1-x^2}
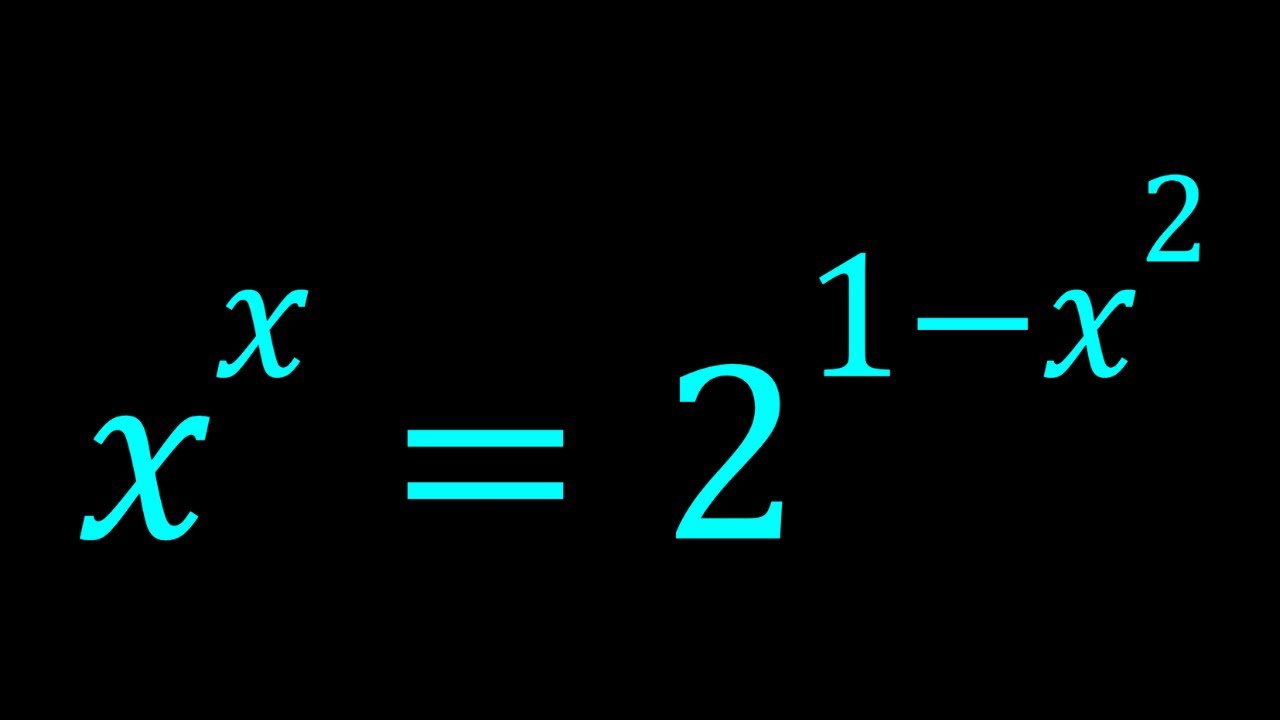
Показать описание
If you need to post a picture of your solution or idea:
#ChallengingMathProblems #ExponentialEquations
via @YouTube @Apple @Desmos @NotabilityApp
@googledocs @canva
PLAYLISTS 🎵 :
#ChallengingMathProblems #ExponentialEquations
via @YouTube @Apple @Desmos @NotabilityApp
@googledocs @canva
PLAYLISTS 🎵 :
Solving the Exponential Equation x^x=2^{1-x^2}
A Nice Exponential Equation, x²=2ˣ
A Homemade Exponential Equation, x^x=2^{1/x}
Nice Olympiad Exponential Equation X^x=2^64 | Solve In 1 Minute
How to Solve the Exponential Equation (1/2)^x = 1/8
Solve the Exponential Equation 2^2x+3 + 1 = 9x2^x
2 different exponential equations
Exponential Equation | 2^(3x+1) - 3(2^2x) + 2^(x+1) = 2^x
Solve a hard exponential equation | #maths
Can you solve this? | Exponential Equation | Algebra Problem.
Solve exponential equation 4^(2x -1) = 7^(x+2). Logarithms
Learn How to Solve Exponential Equations Using Two Different Methods | Step-by-Step Tutorial
Solving the Exponential Equation 6^(x - 2) = 1
How do I find x? Exponential equation with two different bases. Reddit precalculus r/Homworkhelp
How to Solve 2^(x - 2) = 3^(2x - 4) Exponential Equation with Different Base with Logarithms
Exponential Equations - Algebra and Precalculus
Exponential equation | Find X in 2^(x-1) + 2^(x+1)=1280 algebraic problem| Algebra | Mathematics
Solving an Exponential Equation (1/8)^(x + 2) = 32^x
Exponential Equations With Powers of X
Exponential Equation | 2²ˣ⁺¹-9(2ˣ)+4=0
Math Olympiad Question | Solve the Exponential Equation 3^x=2^(x+1) | Math Olympiad Training
Solving the Exponential Eqn. 9^x+6^x=2^{2x+1}
How do you solve an exponential equation with e as the base
Solving the Exponential Equation 5^(2x + 1) = 25
Комментарии
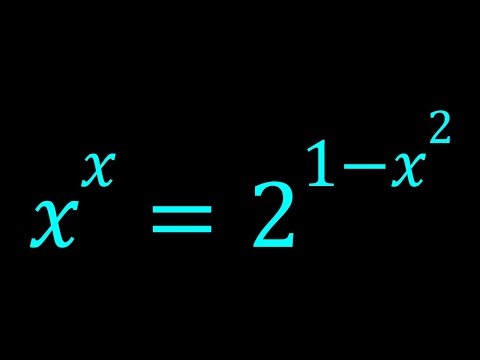 0:08:49
0:08:49
 0:10:34
0:10:34
 0:10:39
0:10:39
 0:01:37
0:01:37
 0:01:03
0:01:03
 0:07:24
0:07:24
 0:09:19
0:09:19
 0:04:44
0:04:44
 0:00:58
0:00:58
 0:03:33
0:03:33
 0:02:43
0:02:43
 0:12:15
0:12:15
 0:00:47
0:00:47
 0:07:47
0:07:47
 0:05:06
0:05:06
 0:05:58
0:05:58
 0:04:28
0:04:28
 0:02:08
0:02:08
 0:05:22
0:05:22
 0:03:39
0:03:39
 0:04:03
0:04:03
 0:05:03
0:05:03
 0:02:47
0:02:47
 0:01:02
0:01:02