filmov
tv
Sampling Distributions: Deriving the Mean and Variance of the Sample Mean

Показать описание
I derive the mean and variance of the sampling distribution of the sample mean.
Sampling Distributions: Deriving the Mean and Variance of the Sample Mean
The Sampling Distribution of the Sample Mean (fast version)
Introduction to sampling distributions | Sampling distributions | AP Statistics | Khan Academy
Sampling Distributions (7.2)
Deriving the Mean and Variance of the Sample Mean
Central Limit Theorem - Sampling Distribution of Sample Means - Stats & Probability
The Sampling Distribution of the Sample Mean
Sample Mean and Population Mean - Statistics
Statistics for Data Science_II Live Stream
Sampling Distributions: Introduction to the Concept
Deriving Distribution of Sample Mean and Sample Variance
Sampling distribution of sample proportion part 1 | AP Statistics | Khan Academy
Sampling distribution of the sample means (Normal distribution) | ExamSolutions
7.2 Sampling Distribution of the Mean (Updated)
Sampling Distribution - Central Limit Theorem - Normal Distribution
Example of Sampling Distribution of the Mean
Lesson 6-4: Sampling Distributions and Estimators
The Sampling Distribution of the Sample Proportion
Proof that the Sample Variance is an Unbiased Estimator of the Population Variance
Sampling Distribution
Finding the Mean and Variance of the sampling distribution of a sample means
Sampling distribution example problem | Probability and Statistics | Khan Academy
Sampling Distributions Excel
The Sample Variance and its Chi Squared Distribution
Комментарии
 0:04:46
0:04:46
 0:07:25
0:07:25
 0:07:18
0:07:18
 0:11:06
0:11:06
 0:05:07
0:05:07
 1:01:09
1:01:09
 0:11:40
0:11:40
 0:05:04
0:05:04
 2:13:42
2:13:42
 0:07:52
0:07:52
 0:23:45
0:23:45
 0:09:57
0:09:57
 0:09:08
0:09:08
 0:13:05
0:13:05
 0:03:11
0:03:11
 0:04:28
0:04:28
 0:19:43
0:19:43
 0:09:49
0:09:49
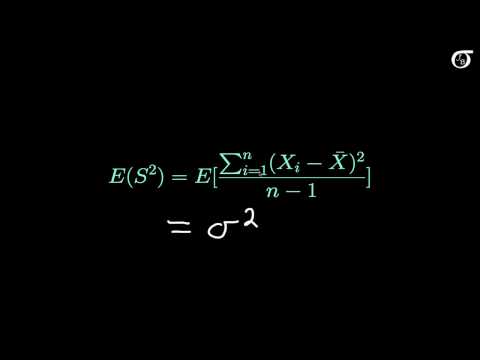 0:06:58
0:06:58
 0:01:16
0:01:16
 0:13:06
0:13:06
 0:14:28
0:14:28
 0:02:47
0:02:47
 0:07:48
0:07:48