filmov
tv
Deriving the Mean and Variance of the Sample Mean
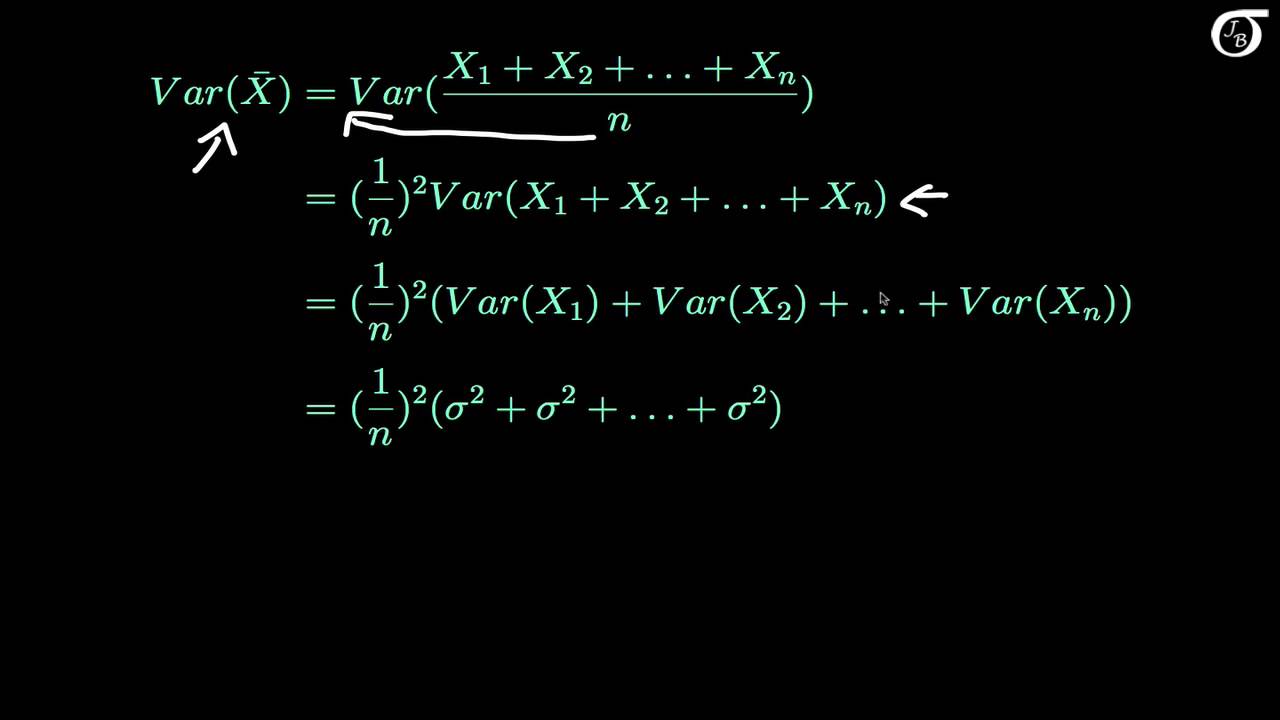
Показать описание
Deriving the Mean and Variance of the Sample Mean
Deriving the Mean and Variance of a Continuous Probability Distribution
Calculating the Mean, Variance and Standard Deviation, Clearly Explained!!!
The Binomial Distribution: Mathematically Deriving the Mean and Variance
Deriving the mean and variance of the least squares slope estimator in simple linear regression
Sampling Distributions: Deriving the Mean and Variance of the Sample Mean
The Bernoulli Distribution: Deriving the Mean and Variance
The Poisson Distribution: Mathematically Deriving the Mean and Variance
Find the Mean and Variance of a Random Variable Given the Probability Density Function
Standard Deviation Formula, Statistics, Variance, Sample and Population Mean
Expected Value and Variance of Discrete Random Variables
Proof that the Sample Variance is an Unbiased Estimator of the Population Variance
How To Calculate Variance
Prove: Variance Shortcut Method for Discrete Random Variable
Mean and variance of Binomial Distribution - A simple proof
Find the Mean, Variance, and Standard Deviation Given the Probability Density Function
MEAN, VARIANCE, AND STANDARD DEVIATION FOR UNGROUPED DATA
Deriving a Confidence Interval for a Variance (Assuming a Normally Distributed Population)
Uniform Distribution Mean and Variance Proof
How To Calculate The Sample Variance | Introduction to Statistics
The Sample Variance: Why Divide by n-1?
Normal Distribution Mean and Variance Proof
HyperGeometric Distribution - Derivation of Mean and Variance (English)
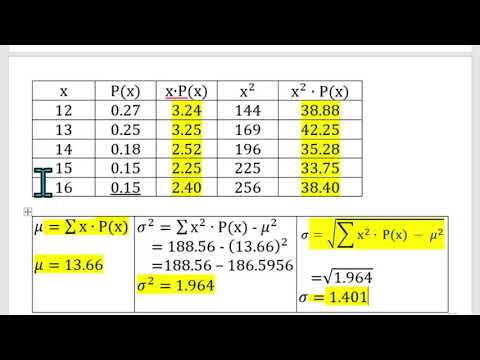
Computing the Mean, Variance and Standard Deviation of a Discrete Probability Distribution Example 2
Комментарии
 0:05:07
0:05:07
 0:07:22
0:07:22
 0:14:22
0:14:22
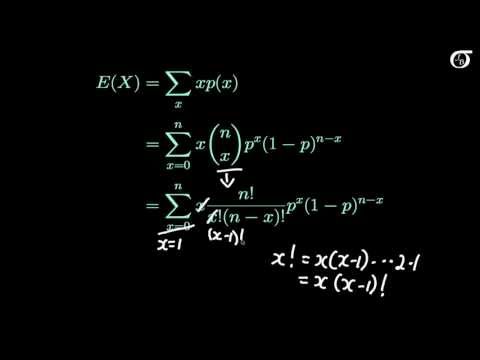 0:13:54
0:13:54
 0:10:54
0:10:54
 0:04:46
0:04:46
 0:03:12
0:03:12
 0:09:17
0:09:17
 0:07:36
0:07:36
 0:10:21
0:10:21
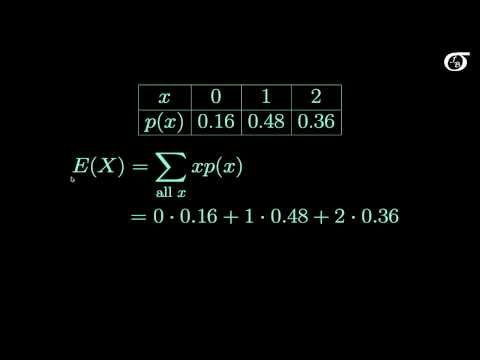 0:07:57
0:07:57
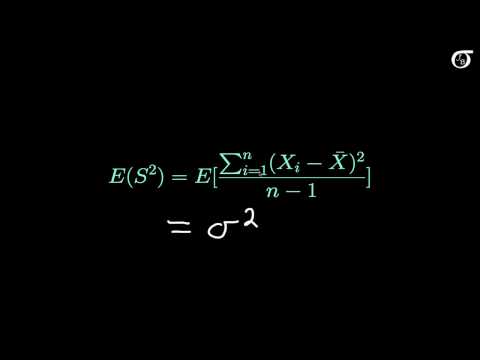 0:06:58
0:06:58
 0:10:24
0:10:24
 0:05:57
0:05:57
 0:07:41
0:07:41
 0:09:38
0:09:38
 0:05:31
0:05:31
 0:04:18
0:04:18
 0:08:37
0:08:37
 0:02:48
0:02:48
 0:06:53
0:06:53
 0:09:29
0:09:29
 0:31:35
0:31:35
 0:09:57
0:09:57