filmov
tv
Find a and b if f(x) is continuous everywhere

Показать описание
In this video , I showed how to use to the continuity coondition to find unknowns for a piecewise function
Find a and b if f(x) is continuous everywhere
Find the values a and b that make the piecewise function continuous
Find the values a and b that make the function differentiable
Find the Values of a and b Such That the Piecewise Function is Differentiable Everywhere (Calculus)
If f(x) = ax + b, f(-1) = -1, f(3) = 1 find the values of a and b and then find f(x)
How to Find a and b so that the Piecewise Function is Continuous Everywhere
If a - b = 7 and ab = 18 ; Find a + b = ? 💡 Olympaid maths problem with solution 💡 IMO 💡
Find a and b
EXCLUSIVE First Look at the New-Tooled RTR Mica B Van from KR Models
SHORTCUT - HOW TO FIND A AND B THAT MAKE PIECEWISE FUNCTION CONTINUOUS EVERYWHERE
Calculus I: Continuity problem: Find a and b so that f is continuous everywhere
How to find the value of a and b if (√7 - 2)/(√7 + 2) = a√7 + b
Find a and b if the number 14ab52343 is Divisible by 37 SSC CAT
If (1 - i/1 + i)^100 = a + ib Find a and b
IF a^2 - b^2 = 25 & ab = 30, Then Find The Value of a +b = ?
Find a and b for Piecewise Function to be Continuous
if A:B=2:3 B:C=4:5 Find A:B:C
If sin(A+B) = 1 and cos(A-B) = 1 find A and B
Find a + b = ? if a^3 + b^3 - 3ab =1 | Olympiad Question
If A:B = 4:5 and B:C = 7:8, then find A:C ?
If a2+b2=41 and ab = 20 find a+b a-b a and b
If 18, a, (b - 3) are in AP, then find value of (2a - b)
find the values of a,b if ax^2+bxy+3y^2-5x+2y-3=0 represents a circle also find the radius andcentre
Find the values of constants a and b when x- 2 and x + 3 both are the factors of expression x^3+...
Комментарии
 0:10:36
0:10:36
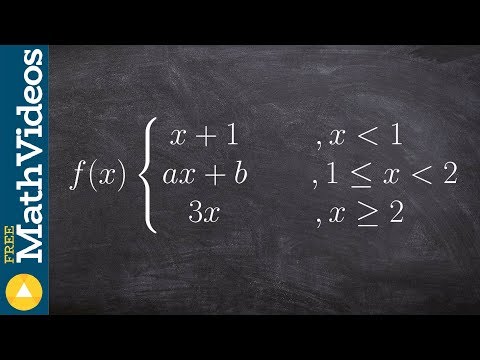 0:03:44
0:03:44
 0:06:05
0:06:05
 0:04:01
0:04:01
 0:03:20
0:03:20
 0:10:48
0:10:48
 0:01:32
0:01:32
 0:08:00
0:08:00
 0:12:08
0:12:08
 0:06:27
0:06:27
 0:10:41
0:10:41
 0:04:24
0:04:24
 0:09:07
0:09:07
 0:06:33
0:06:33
 0:04:18
0:04:18
 0:06:08
0:06:08
 0:00:47
0:00:47
 0:03:46
0:03:46
 0:11:34
0:11:34
 0:00:54
0:00:54
 0:03:21
0:03:21
 0:03:05
0:03:05
 0:01:01
0:01:01
 0:05:55
0:05:55