filmov
tv
Measure Theory 6 | Lebesgue Integral

Показать описание
Please consider to support me if this video was helpful such that I can continue to produce them :)
🙏 Thanks to all supporters! They are mentioned in the credits of the video :)
This is part 6 of 22 videos.
#MeasureTheory
#Analysis
#Integral
#Calculus
#Measures
#Mathematics
#Probability
I hope that this helps students, pupils and others. Have fun!
(This explanation fits to lectures for students in their first and second year of study: Mathematics for physicists, Mathematics for the natural science, Mathematics for engineers and so on)
Measure Theory: Part 6 Lebesgue integral
A horizontal integral?! Introduction to Lebesgue Integration
[79] Intro to Lebesgue Measure & Lebesgue Integral (Baby Rudin Chapter 2 Set Theory #5) #4.3.2.2...
Music And Measure Theory
Measure Theory, Functional Analysis, and The Lebesgue Integral for Undergraduates - Johnston
#RealAnalysis #LEBESGUE MEASURE THEORY & INTEGRATION by (p.k Jain .) for b.sc.& m.sc. mathem...
Measure theory Section 3.1/Example 6
Lecture 8: Lebesgue Measurable Subsets and Measure
Measure Theory 6: Lebesgue Outer Measure-2: Cantor Set-1
SIT3001 Week 6 (The Lebesgue integral)
Measure Theory 13 | Lebesgue-Stieltjes Measures
Real analysis Lebesgue measure lec.6
#6 lebesgue integral
Measure Theory (6/15) - Collections of sets - part 2 of 2
LEBESGUE MEASURE
msc. Maths ( Lebesgue Measure and Integration)
MEASURE THEORY: Lebesgue Measurable Set and its Properties
The most important measure in R - Lebesgue Measure | Measure Theory
Functional Analysis #6: Lebesgue Outer Measure
Functional Analysis #7: The Lebesgue Measure
Measure Theory 23 Lebesgue Integral - 6: Integration of Complex valued Functions
Measure and integration Lecture 6 Lebesgue measurable sets (part II)
Lecture 6 (Part 4): Lebesgue measure as a consequence of Caratheodry theorem
Live Session-6(Measure theory and Integration)
Комментарии
 0:23:02
0:23:02
 0:09:54
0:09:54
![[79] Intro to](https://i.ytimg.com/vi/EKoXPQwrOiU/hqdefault.jpg) 0:37:07
0:37:07
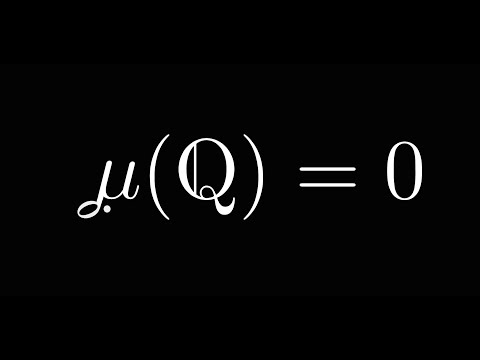 0:13:13
0:13:13
 0:15:46
0:15:46
 0:00:16
0:00:16
 0:05:41
0:05:41
 1:14:02
1:14:02
 0:49:48
0:49:48
 1:33:35
1:33:35
 0:13:55
0:13:55
 0:52:40
0:52:40
 0:07:30
0:07:30
 0:07:56
0:07:56
 0:17:30
0:17:30
 0:01:16
0:01:16
 0:22:15
0:22:15
 0:12:52
0:12:52
 0:21:25
0:21:25
 0:35:42
0:35:42
 0:48:14
0:48:14
 1:00:24
1:00:24
 0:30:27
0:30:27
 2:13:26
2:13:26