filmov
tv
Measure Theory 13 | Lebesgue-Stieltjes Measures
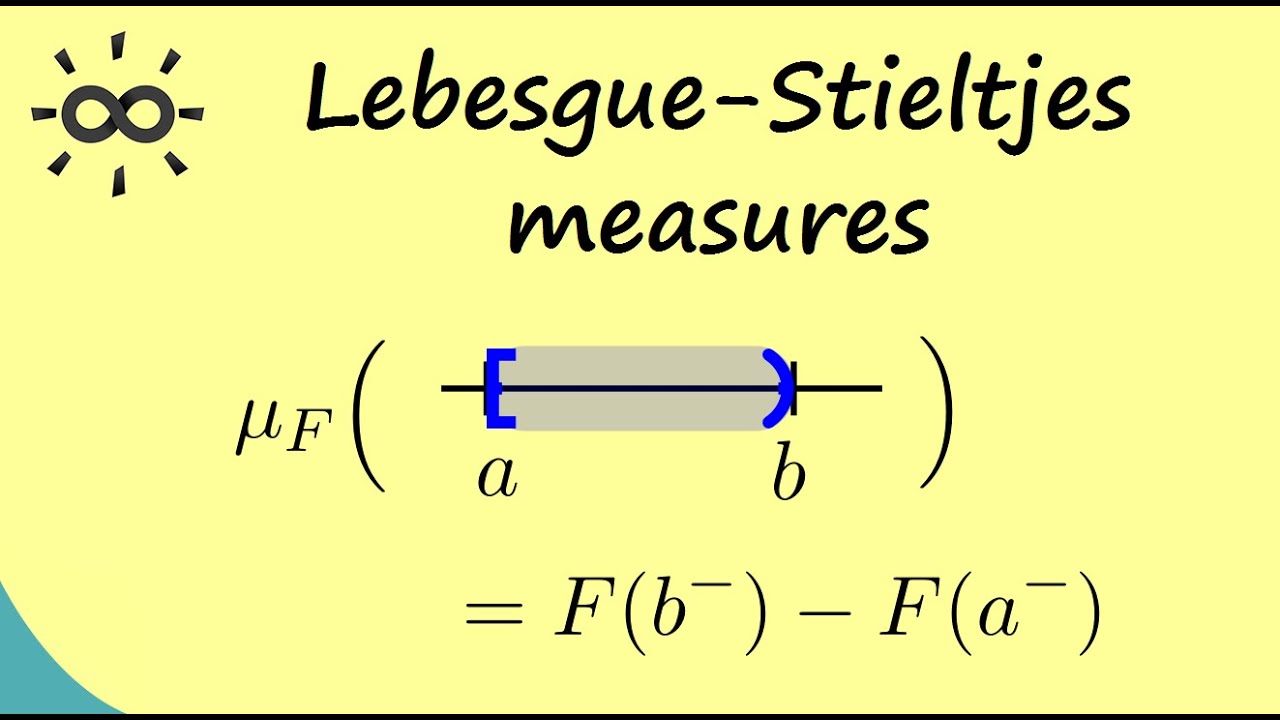
Показать описание
Please consider to support me if this video was helpful such that I can continue to produce them :)
🙏 Thanks to all supporters! They are mentioned in the credits of the video :)
This is part 13 of 22 videos.
#MeasureTheory
#Analysis
#Integral
#Calculus
#Measures
#Mathematics
#Probability
I hope that this helps students, pupils and others. Have fun!
(This explanation fits to lectures for students in their first and second year of study: Mathematics for physicists, Mathematics for the natural science, Mathematics for engineers and so on)
Measure Theory 13 | Lebesgue-Stieltjes Measures
Measure Theory 13 | Lebesgue-Stieltjes Measures [dark version]
Measure Theory: Part 13 Lebesgue Stieltjes Measures
Maßtheorie - Teil 13 - Lebesgue-Stieltjes-Maße
Maßtheorie - Part 13 - Lebesgue-Stieltjes-Maße
Are Lebesgue-Stieltjes measures Borel regular? Proof | Measure Theory
ST342 023 Lebesgue measure and Lebesgue Stieltjes measures 1 of 2
A horizontal integral?! Introduction to Lebesgue Integration
Motivation for Lebesgue-Stieltjes Measures | Motivation | Measure Theory
Lecture 18. Lebesgue-Stieltjes integration
Probability and Measure, Lecture 7: Lebesgue-Stieltjes Measure and Monotone Classes
Lebesgue measure explained with simple example
Lebesque-Stieltjes Integral
Math of QM: Appendix on Lebesgue-Stieltjes Integrals, part 1
27 Lebesgue Measure, Riemann and Lebesgue Integrals by Home of Mathematics
The most important measure in R - Lebesgue Measure | Measure Theory
Probability and Measure, Lecture 7: Lebesgue-Stieltjes Measure and Monotone Classes
Lebesgue Integration 5: Important/Useful Results
Analysis Lecture 13: Sets of Measure Zero
3.1 Stieltjes Premeasures
Lecture 23 : Lebesgue-Stieltjes Measures
Lecture 35 : Computations involving Lebesgue Integration
2.5 - Construction of the Lebesgue measure
L02 4 Lebesgue measure
Комментарии
 0:13:55
0:13:55
 0:14:10
0:14:10
 0:13:55
0:13:55
 0:12:02
0:12:02
 0:12:02
0:12:02
 0:24:00
0:24:00
 0:05:32
0:05:32
 0:09:54
0:09:54
 0:09:26
0:09:26
 1:10:37
1:10:37
 1:27:41
1:27:41
 0:13:24
0:13:24
 0:08:32
0:08:32
 0:19:09
0:19:09
 0:04:22
0:04:22
 0:12:52
0:12:52
 1:27:41
1:27:41
 0:12:46
0:12:46
 0:06:37
0:06:37
 0:25:54
0:25:54
 0:32:03
0:32:03
 0:35:47
0:35:47
 0:22:02
0:22:02
 0:14:19
0:14:19