filmov
tv
LEBESGUE MEASURE

Показать описание
A horizontal integral?! Introduction to Lebesgue Integration
The most important measure in R - Lebesgue Measure | Measure Theory
Lecture 06: The Lebesgue measure
Music And Measure Theory
Lecture 8: Lebesgue Measurable Subsets and Measure
Measure Theory 13 | Lebesgue-Stieltjes Measures
How to Find the Area of a Triangle Using the Lebesgue Measure
Measure Theory 2.1 : Lebesgue Outer Measure
Lecture 1: An introduction to Lebesgue measure
2.5 - Construction of the Lebesgue measure
Measure Theory 13 | Lebesgue-Stieltjes Measures [dark version]
Lecture 9: Lebesgue Measurable Functions
Lecture 2: Outer measures, construction of the Lebesgue measure.
Lec2 Math611 Lebesgue Outer Measure
Mod-01 Lec-09 BOREL SETS AND LEBESGUE MEASURE-1
Lebesgue measure explained with simple example
L02 4 Lebesgue measure
CSIR NET MATHEMATICS DEC 2017 | Real Analysis | Lebesgue Measure of a set
LECTURE 1: Summary of the Concept of Length and the Lebesgue Outer Measure.
msc. Maths ( Lebesgue Measure and Integration)
Measurable sets|| Lebesgue Measures
Measure Theory 1.1 : Definition and Introduction
Measure Theory 2.2 : Lebesgue Measure of the Intervals
measure theory/Lebesgue measure theory/L 1/Exterior measure outer measure/interior measure real
Комментарии
 0:09:54
0:09:54
 0:12:52
0:12:52
 0:23:51
0:23:51
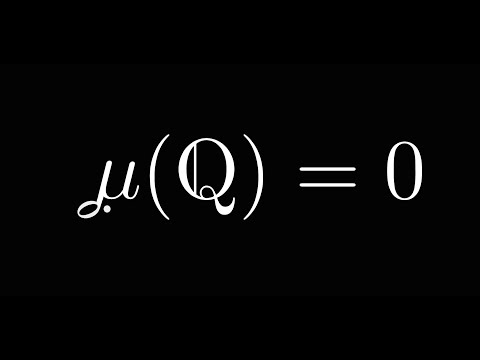 0:13:13
0:13:13
 1:14:02
1:14:02
 0:13:55
0:13:55
 0:01:02
0:01:02
 0:11:00
0:11:00
 0:19:21
0:19:21
 0:22:02
0:22:02
 0:14:10
0:14:10
 1:24:57
1:24:57
 1:07:41
1:07:41
 1:00:27
1:00:27
 0:50:11
0:50:11
 0:13:24
0:13:24
 0:14:19
0:14:19
 0:07:31
0:07:31
 0:40:46
0:40:46
 0:01:16
0:01:16
 0:23:32
0:23:32
 0:09:30
0:09:30
 0:13:25
0:13:25
 0:51:11
0:51:11