filmov
tv
Limit of sinx/x^(1/3) as x approaches 0 | Calculus 1 Exercises

Показать описание
We evaluate the limit of sinx/cube root x by multiplying by x^(1/3)^2/x^(1/3)^2, which allows us to take a sinx/x out of the limit statement. As we know, the limit of sinx/x as x approaches 0 is 1!
Join Wrath of Math to get exclusive videos, music, and more:
◉Textbooks I Like◉
★DONATE★
Thanks to Loke Tan, Raül Beienheimer, Matt Venia, Micheline, Doug Walker, Odd Hultberg, Marc, Shlome Ashkenazi, Barbora Sharrock, Mohamad Nossier, Rolf Waefler, Shadow Master, and James Mead for their generous support on Patreon!
Outro music is mine. You cannot find it anywhere, for now.
Follow Wrath of Math on...
Join Wrath of Math to get exclusive videos, music, and more:
◉Textbooks I Like◉
★DONATE★
Thanks to Loke Tan, Raül Beienheimer, Matt Venia, Micheline, Doug Walker, Odd Hultberg, Marc, Shlome Ashkenazi, Barbora Sharrock, Mohamad Nossier, Rolf Waefler, Shadow Master, and James Mead for their generous support on Patreon!
Outro music is mine. You cannot find it anywhere, for now.
Follow Wrath of Math on...
Limit of sinx/x^(1/3) as x approaches 0 | Calculus 1 Exercises
Limits Using Sinx/x =1
02 Fundamental Limit of Trigonometric Function Proof sinx/x as x approaches zero
Proof: Limit of sinx/x as x approaches 0 with Squeeze Theorem | Calculus 1
The most important limit in Calculus // Geometric Proof & Applications
Limit of x-sinx/x^3 as x approaches 0
Limits of Trigonometric Functions
Limits: A proof of lim sinx/x =1
L19 KCET 2025 Maths Course | Continuity & Differentiability Complete Revision & PYQs
Proof Lim (sinx)/x = 1 | Limits | Calculus
Limit of (sinx/x)^1/x^2 as x approaches 0
Unusual ways to prove lim sinx/x =1
limit x to 0 of (x-sinx)/x^3
Proof that the Limit as x Approaches 0, sinx/x is 1 or lim x~0, sin(x)/x = 1
Limit of sinx-x/x^3 as x approaches 0
How REAL Men Integrate Functions
5 simple unsolvable equations
Limit of sin(x)/x as x approaches 0 | Derivative rules | AP Calculus AB | Khan Academy
Limit of sinx/x as x approaches 0 (ILIEKMATHPHYSICS)
lim x tends to x-sinx / x^3 = 1/6
Limit using sinx/x as x goes to zero
Limit of sinx/x as x approaches 0
Limit of sinx/x as x goes to 0 #shorts
Limit of sinx^2/x as x approaches 0 | Calculus 1 Exercises
Комментарии
 0:01:51
0:01:51
 0:05:55
0:05:55
 0:02:21
0:02:21
 0:10:21
0:10:21
 0:11:54
0:11:54
 0:01:35
0:01:35
 0:15:23
0:15:23
 0:13:15
0:13:15
 0:59:46
0:59:46
 0:07:33
0:07:33
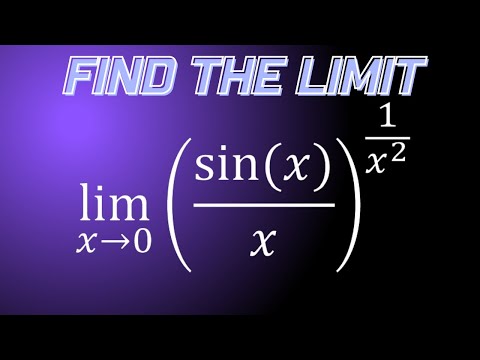 0:04:24
0:04:24
 0:11:17
0:11:17
 0:01:51
0:01:51
 0:05:33
0:05:33
 0:02:12
0:02:12
 0:00:35
0:00:35
 0:00:50
0:00:50
 0:09:16
0:09:16
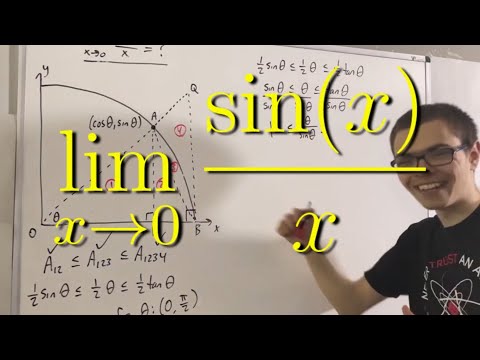 0:12:53
0:12:53
 0:04:15
0:04:15
 0:12:18
0:12:18
 0:04:56
0:04:56
 0:01:00
0:01:00
 0:03:02
0:03:02