Probability Theory 10 | Random Variables

Please consider to support me if this video was helpful such that I can continue to produce them :)

🙏 Thanks to all supporters! They are mentioned in the credits of the video :)

This is my video series about Probability Theory. I hope that it will help everyone who wants to learn about it.
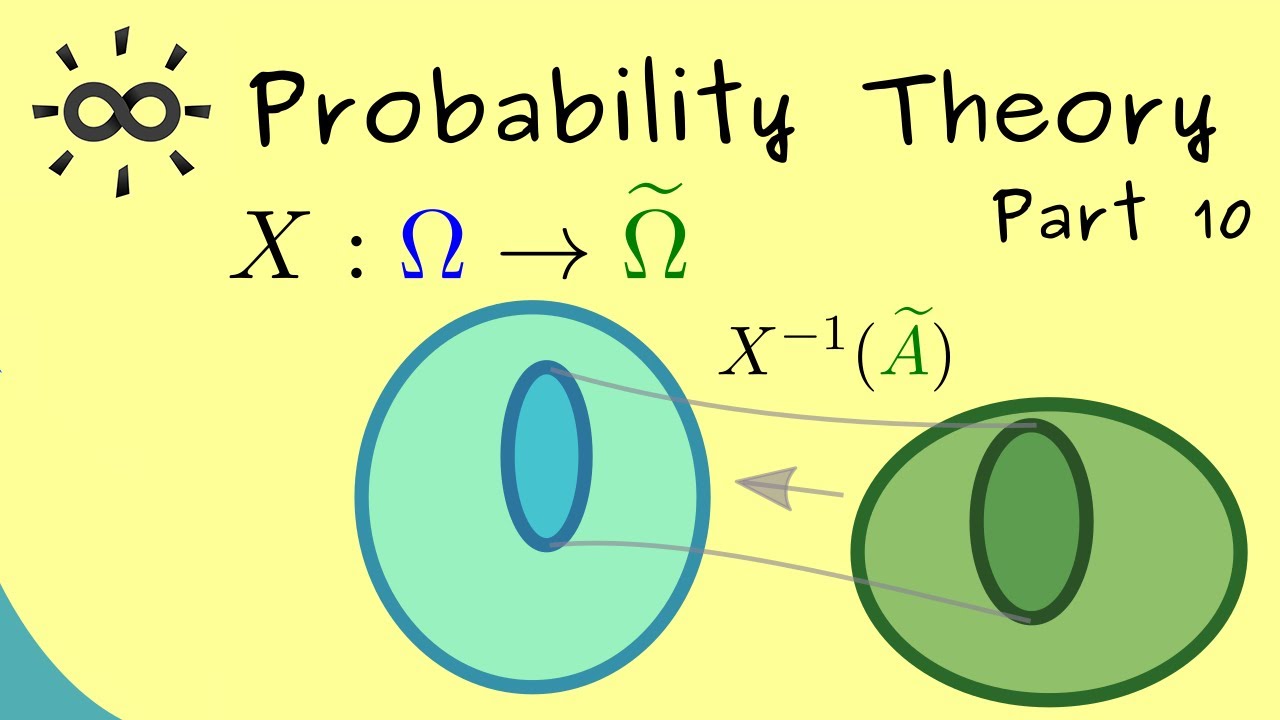
This video is about probability theory, also known as stochastics, stochastic processes or statistics. I keep the title in this general notion because I want cover a lot of topics with the upcoming videos.

Here we talk about the important concept of random variables. We use the general definition between arbitrary measurable spaces, but we mostly discuss real-valued random variables as the occur in applications.

00:00 Intro/ short introduction
00:56 Example (discrete)
02:57 Definition of a random variable
04:56 Continuation of the example
07:49 Notation
09:28 Outro

#ProbabilityTheory
#Analysis
#Calculus
#Mathematics

I hope that this helps students, pupils and others. Have fun!

(This explanation fits to lectures for students in their first and second year of study: Mathematics for physicists, Mathematics for the natural science, Mathematics for engineers and so on)

[jaimelima]

Thanks for putting this together. It will helpful for a lot of people. Probability theory is littered with conflicting terminologies and several times during the applied courses the concepts are not explained in full to make them consistent in mathematical terms. These strategic bridges you are building between the more abstract Measure Theory and Probability Theory are really useful to reconcile some concepts in my mind.

[treywilkinson]

The connection you provide between probability theory and measure theory has helped me so much. I appreciate your effort!

[Gouleur]

You're knocking it out of the park with this series, can't wait for the next episode!

[zhizhongpu]

why did you say the choice of A~ does not matter at all? at 5:28

[jsoldi]

In example (a) the sigma algebra of the second set is the borel algebra, does that mean our probability function will give probabilities of intervals and not of individual sums? I was assuming if we pass the function, for example, {2, 12} we'd get 2/36, but if we use borel algebra then that'd be interpreted as an interval, so the output of the function would be just 1. Is this correct? And if so, could we have not used borel algebra on the right side if we wanted to distinguish between individual elements, for instance, if we want P({2, 4}) to be different from P({2, 3, 4})?

Hello Julian!
As always, exceptional videos and explanations!
The pace now (IMHO) is perfect - you left a small pause after you finish a concept, that is perfect.
I have one question: if I want to prove that a function is measurable, is it enough to show that the pre-image of ATOMS of the sigma-algebra on the right (these "right-atoms" would be only the images of the atoms of the sigma-algebra on the left) belong to omega (the set on the left)?

[umbranocturna]

Thank you so much, this is so much easier to understand than what my University is telling me.

[teddysariel]

If I'm not mistaken, the last notation remark should involve A \in \tilde{A}, and not \tilde{A} itself.
Thanks for the video, and for your work in general.

[rombo]

So clear. Italian maths books are very theoretical and I literally have headaches when I try to study on them. This video tho... CLEAR without it being informal! Thanks.

[molibdenum]

At 9:15, why did you say that the left side P(X element of A~) "does not make sense" by itself and is just shortcut defined as the rightmost expression? Woudn't we also be interested in the probability over the random variable also, like P(sum of throws >= 10) = P(X element of [10, 12]?

[skillick]

Thank you, the notation in probability theory is confusing-your videos make it much more clear.

[hn]

Could you please explain 6:09 again? Why is this trivially fulfilled? Thank you.

[musicalBurr]

A possibly dumb question coming, but first, let me say how much I have enjoyed your channel over the years! Thanks so much. Ok, dumb question now:

Say I have X^-1({2.5}) (or something not the sum of the two dice), then I take it that it's pre-image set is {} (i.e. empty set) which IS an element of P(omega), is this right?

To continue, is this also correct (using range of real numbers): X^-1([1.5, 3.5]) = {(1, 1), (1, 2), (2, 1)}?

Thanks again!

[lueelee]

I thought one mainly used [] to denote image and pre images of functions as to avoid confusion with functions with ().