filmov
tv
Solving m^2=n^3+k^2 (partially) for Positive Integers

Показать описание
If you need to post a picture of your solution or idea:
#NumberTheoryProblems #DiophantineEquations
EXPLORE 😎:
PLAYLISTS 🎵 :
#NumberTheoryProblems #DiophantineEquations
EXPLORE 😎:
PLAYLISTS 🎵 :
Solving m^2=n^3+k^2 (partially) for Positive Integers
Solve a Linear Congruence with common factor
Quadratic Equations IIT Questions No 05 ( X Class)
Most💯 Important Step Before any Procedure 🔥
Solving congruences, 3 introductory examples
Partial sums intro | Series | AP Calculus BC | Khan Academy
asking minor test marks to allen topper allen kota #allen #allenkota #physicswallah #pw
🔥 POV: Integration - Look at me! 👀 💪 | JEE 2024 | Math | Bhoomika Ma'am
what is sigma notation and how to we use it
Find the sum of first n squares, difference equation approach, (ft. Max!)
Solving a consecutive integer problem algebraically | Linear equations | Algebra I | Khan Academy
Proof by Induction : Sum of series ∑r² | ExamSolutions
Functions IIT Questions NO 11 ( X Class)
One minus one plus one minus one - Numberphile
how to setup partial fractions (all cases)
Math tutorial for solving rational equations
Congruence Modulo m
How to Reset SMC on Macbook Pro - Fix loud fans, slow loading, keyboard backlight
Difference Between Partial and Total Derivative
How to Factor and Solve Quadratics - Sneaky Trick - No Fuss Factoring
Partial Differential Equation :solution of one dimensional wave equation
Why is pi here? And why is it squared? A geometric answer to the Basel problem
Crystallization Experiment - Grow Salt Crystals | DIY Science Project
But what is a partial differential equation? | DE2
Комментарии
 0:07:29
0:07:29
 0:02:21
0:02:21
 0:00:57
0:00:57
 0:00:16
0:00:16
 0:03:51
0:03:51
 0:06:08
0:06:08
 0:00:30
0:00:30
 0:00:48
0:00:48
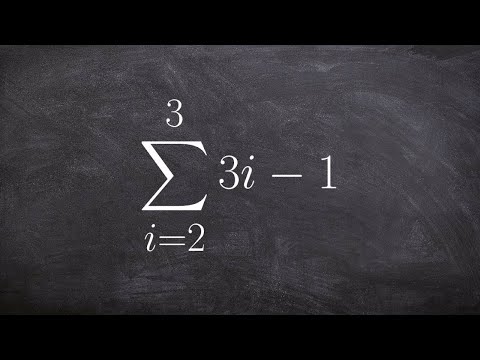 0:01:22
0:01:22
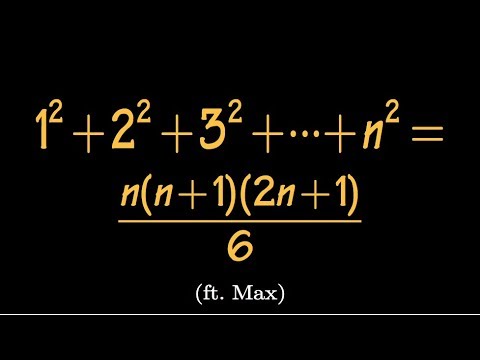 0:11:19
0:11:19
 0:05:19
0:05:19
 0:08:16
0:08:16
 0:00:48
0:00:48
 0:11:10
0:11:10
 0:09:08
0:09:08
 0:06:32
0:06:32
 0:12:13
0:12:13
 0:00:42
0:00:42
 0:01:44
0:01:44
 0:05:42
0:05:42
 0:19:15
0:19:15
 0:17:08
0:17:08
 0:00:39
0:00:39
 0:17:39
0:17:39