filmov
tv
how to setup partial fractions (all cases)
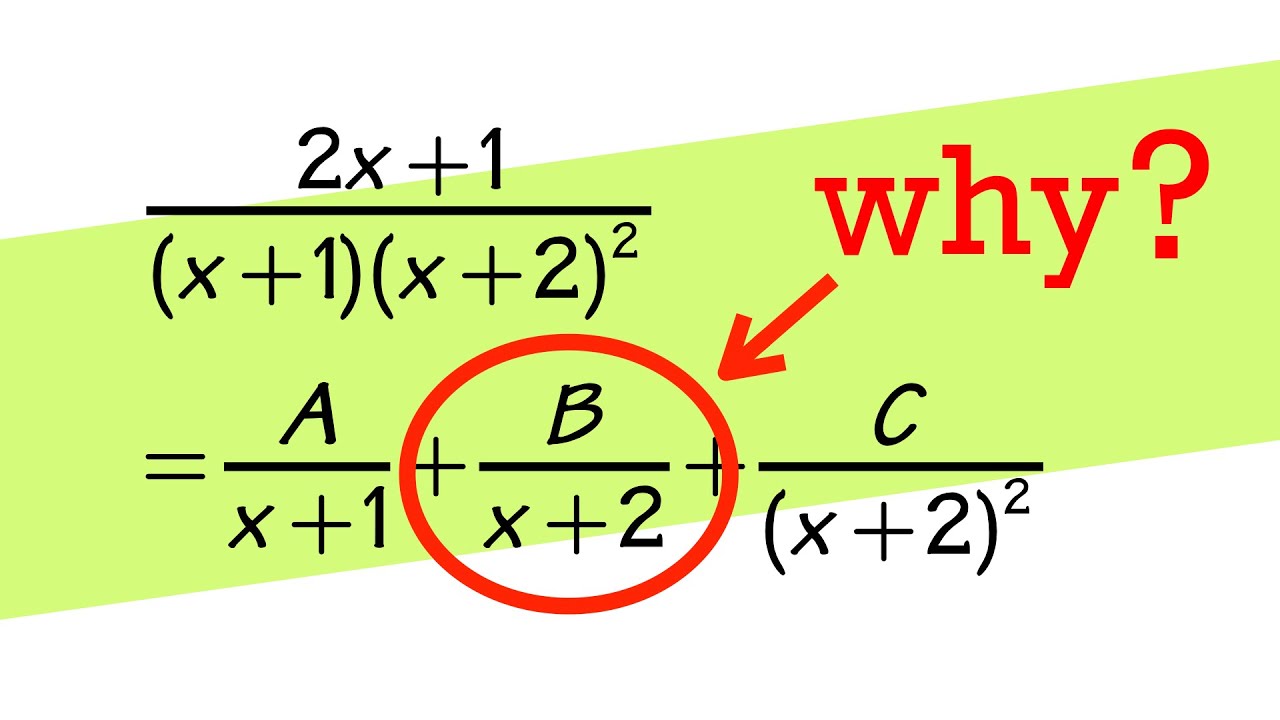
Показать описание
-----------------------------
-----------------------------
-----------------------------
how to setup partial fractions (all cases)
Partial Fraction Decomposion
How to Set Up the Partial Fraction Decomposition
Ultimate Partial Fraction Decomposition Study Guide (how setup)
Integration By Partial Fractions
Partial Fraction Decomposition (How to Set Up)
Partial Fraction Decomposition All Types
Introduction To Partial Fractions
Partial Fractions - Denominator with quadratic factors | SHS 1 ELECTIVE MATH
how to solve partial fractions
This is how we partial fraction, repeated linear roots, 'cover-up method'
Ex: Setting Up Partial Fraction Decomposition
Re-writing This Integral and using Partial Fraction Decomposition #calculus #calculushelp #integrals
A faster method to do partial fractions! See this!
Partial Fractions
Partial fractions
Calculus 2 Lecture 7.4: Integration By Partial Fractions
This is how we partial fraction, repeated linear factors, 'build up the power'
Free Ecet Logics || Techniques||Partial Fractions Short Cut#2
Partial Fraction Decomposition ( 6 Worked Examples)
We don't always need partial fractions!!
Set Up the Partial Fraction Decomposition
Calculus 2: how to NOT do partial fractions for the integrals (2 examples)
Integration By Partial Fractions (irreducible quadratic factors)
Комментарии
 0:09:08
0:09:08
 0:14:12
0:14:12
 0:05:41
0:05:41
 0:11:53
0:11:53
 0:41:07
0:41:07
 0:03:42
0:03:42
 0:32:24
0:32:24
 0:08:54
0:08:54
 0:08:20
0:08:20
 0:14:48
0:14:48
 0:07:58
0:07:58
 0:06:18
0:06:18
 0:00:56
0:00:56
 0:01:00
0:01:00
 0:00:05
0:00:05
 0:14:24
0:14:24
 2:55:43
2:55:43
 0:10:43
0:10:43
 0:00:54
0:00:54
 0:44:29
0:44:29
 0:00:44
0:00:44
 0:07:03
0:07:03
 0:05:48
0:05:48
 0:19:09
0:19:09