Multivariable calculus, class #13: optimizing on a constrained region

Mathematician spotlight: Kathryn Lindsey

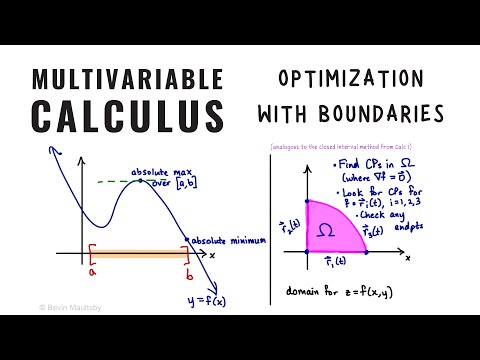
We start with a map of the 50 United States, which has the highest and lowest point of every state marked. We determine that every high point occurs on the interior, along an edge, or at a corner. We do two examples of optimizing a polynomial function on a closed, bounded region. The first is a rectangle, so we have to parameterize each boundary curve separately, and test the corners. The second is an ellipse, so the boundary is a single curve, and there are no corners. We also show a clever trick for reducing this one to a function of one variable by solving the constraint curve for one of the variables and plugging into the function.