filmov
tv
Solving an exponential equation with e on the denominator
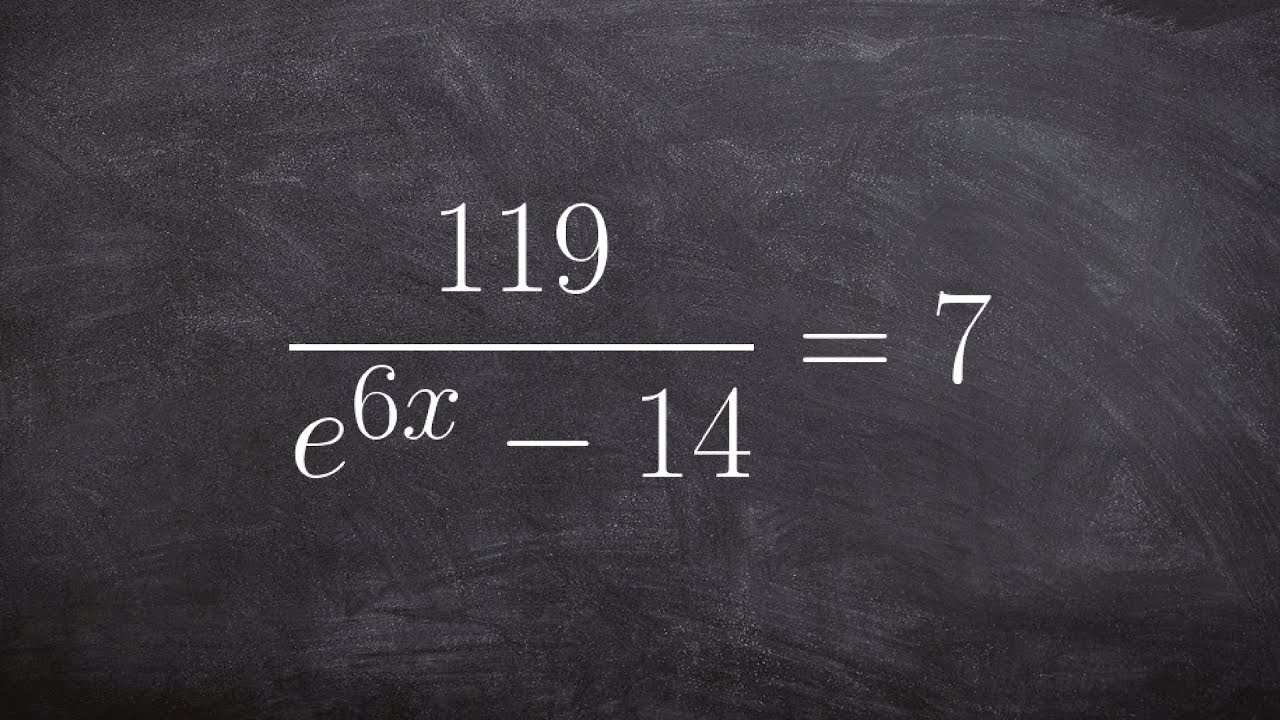
Показать описание
👉 Learn how to solve exponential equations in base e. An exponential equation is an equation in which a variable occurs as an exponent. e is a mathematical constant approximately equal to 2.71828. e^x is a special type of exponential function called the (natural) exponential function
To solve a natural exponential equation, we use the properties of exponents to isolate the (natural) exponential functions. Then we take the natural log of both sides. Note that the natural log cancels out the (natural) exponential function (e), leaving out only the exponent.
Organized Videos:
✅Solve Exponential Equations
✅Solve Exponential Equations | Learn About
✅Solve Exponential Equations with a Calculator
✅Solve Exponential Equations with Fractions
✅Solve Exponential Equations | Easy
✅Solve Exponential Equations with e
✅Solve Exponential Equations with Logarithms
✅Solve Exponential Equations without a Calculator
Connect with me:
#brianmclogan #exponential
To solve a natural exponential equation, we use the properties of exponents to isolate the (natural) exponential functions. Then we take the natural log of both sides. Note that the natural log cancels out the (natural) exponential function (e), leaving out only the exponent.
Organized Videos:
✅Solve Exponential Equations
✅Solve Exponential Equations | Learn About
✅Solve Exponential Equations with a Calculator
✅Solve Exponential Equations with Fractions
✅Solve Exponential Equations | Easy
✅Solve Exponential Equations with e
✅Solve Exponential Equations with Logarithms
✅Solve Exponential Equations without a Calculator
Connect with me:
#brianmclogan #exponential
Solving Exponential Equations
Solving an exponential equation with different bases
Solving an exponential equation
Solving exponential equations with different bases
How do you solve an exponential equation with e as the base
How to solve an exponential equation with two different bases
Solving Exponential Equations
Solving exponential equation | Exponential and logarithmic functions | Algebra II | Khan Academy
Exponential Equation Solution#mathproblem ##squareroot #maths #ytshorts
how to solve an exponential equation with two different bases
Solving Exponential Equation
Solving exponential equations using exponent properties | High School Math | Khan Academy
Exponential Equation Grade 10
Exponential Equations - Algebra and Precalculus
08 - Solving Exponential Equations - Part 1 - Solve for the Exponent
Learn How to Solve Exponential Equations Using Two Different Methods | Step-by-Step Tutorial
Solving Exponential equations
How to Solve Exponential Equations using Logarithms - No Common Base Present
How do I find x? Exponential equation with two different bases. Reddit precalculus r/Homworkhelp
Solving Exponential Equations with Common Bases (Precalculus - College Algebra 54)
Solving Exponential and Logarithmic Equations
Learn how to get the same bases to solve an exponential equation
Solving Exponential Equations - Part 1 of 2
Solving Exponential Equations
Комментарии
 0:16:36
0:16:36
 0:03:01
0:03:01
 0:03:14
0:03:14
 0:04:41
0:04:41
 0:02:47
0:02:47
 0:05:11
0:05:11
 0:01:46
0:01:46
 0:05:12
0:05:12
 0:00:30
0:00:30
 0:03:21
0:03:21
 0:02:56
0:02:56
 0:04:56
0:04:56
 0:01:39
0:01:39
 0:05:58
0:05:58
 0:18:28
0:18:28
 0:12:15
0:12:15
 0:01:52
0:01:52
 0:05:47
0:05:47
 0:07:47
0:07:47
 0:37:06
0:37:06
 0:07:08
0:07:08
 0:02:06
0:02:06
 0:06:28
0:06:28
 0:20:04
0:20:04