filmov
tv
Factoring a septic polynomial. A challenge in algebra
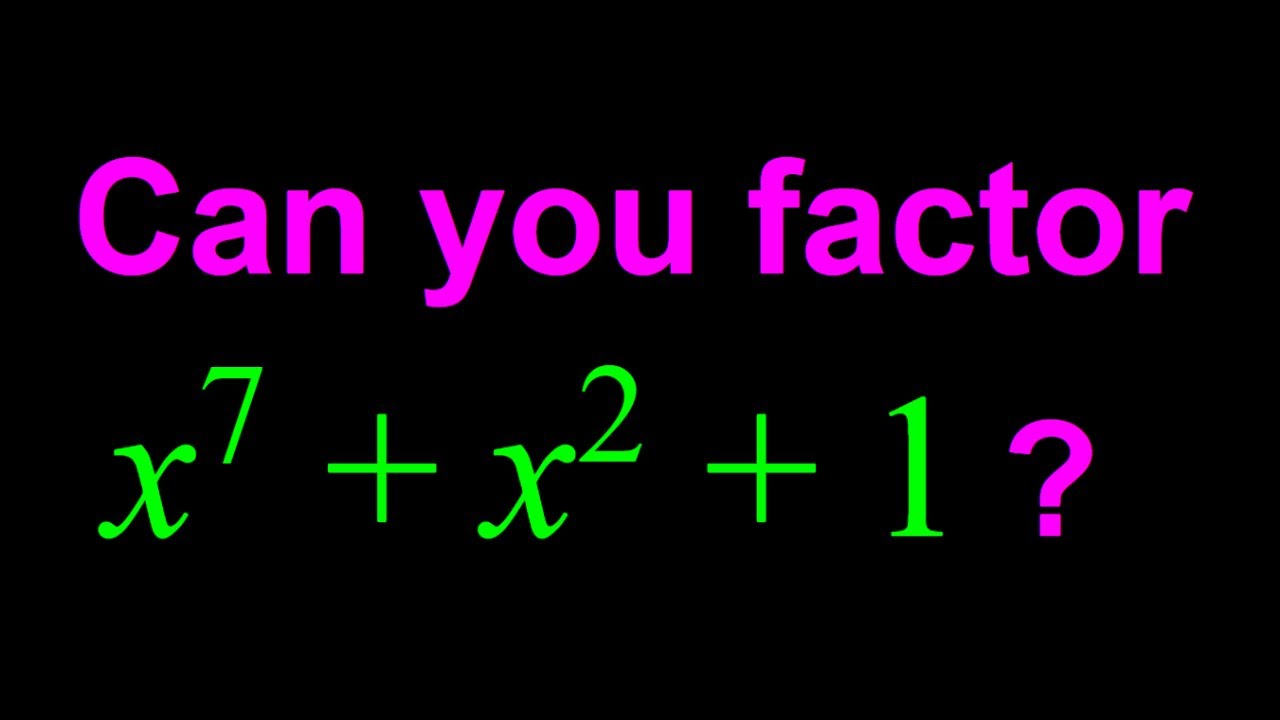
Показать описание
This video is about factoring a polynomial. A challenge in algebra
If you need to post a picture of your solution or idea:
#ChallengingMathProblems #FactoringPolynomials
SIMILAR VIDEOS:
If you need to post a picture of your solution or idea:
#ChallengingMathProblems #FactoringPolynomials
SIMILAR VIDEOS:
Factoring a septic polynomial. A challenge in algebra
Factoring a Septic Polynomial | Algebra Challenge
Factoring a Septic Polynomial | How To Factor A Septic Polynomial | Aman Sir
Simple Way to Solve the Septic Polynomial Equation 16x^7+7x^3+1=0
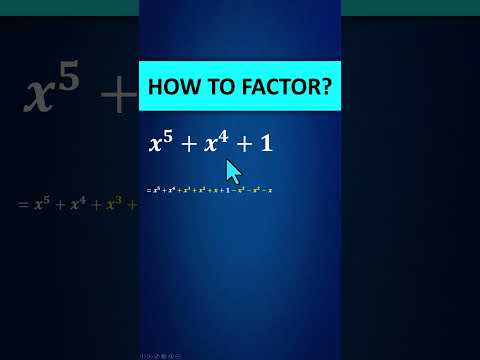
x^5+x^4+1 How to Factor Quintic Polynomial?
A nice septic polynomial maths problem | Are you able to solve it ? |
Factoring a tenth degree polynomial. An algebraic challenge solved in two ways.
An Ecuador Olympiad Challenge | Crack This Septic Equation
x⁷ + x² + 1 | How to factorise x⁷ + x² + 1 Factorization | Factorise | Factoring Septic Equation...
5 simple unsolvable equations
A Challenging Factorization Question (x+1)^4 + (x+3)^4 -272 | Olympiad Math
Solving a septic equation
Factorisation Challenge || a^4 + a^2 + 1 = ?
Solving a Polynomial System
Factoring a thirteenth degree polynomial.
How To Factor A Nice Quartic in Two Different Ways
Factoring a cubic polynomial in two ways
Evaluating a Septic Algebraic Expression in Three Ways
How to Factorise a Septic Polynomial || Special Polynomial || Step by Step Solution by Gopal Sir
Algebra 1. Factoring cubic polynomials. Challenge, real world connection
Factoring a Quintic | Challenging Algebra
Cubic Equation by Factoring
Cool Tricks!! | Solution to the Sextic Equation x^6+2x^5-18x^2-81=0 | Math Olympiad
How to Factor x^11+x^10+x^9+...+x^2+x+1 Maths Olympiad Problem
Комментарии
 0:09:43
0:09:43
 0:09:43
0:09:43
 0:05:54
0:05:54
 0:02:12
0:02:12
 0:00:54
0:00:54
 0:03:45
0:03:45
 0:13:34
0:13:34
 0:09:04
0:09:04
 0:03:09
0:03:09
 0:00:50
0:00:50
 0:08:55
0:08:55
 0:10:43
0:10:43
 0:04:57
0:04:57
 0:00:52
0:00:52
 0:13:24
0:13:24
 0:09:53
0:09:53
 0:12:22
0:12:22
 0:10:48
0:10:48
 0:07:38
0:07:38
 0:04:16
0:04:16
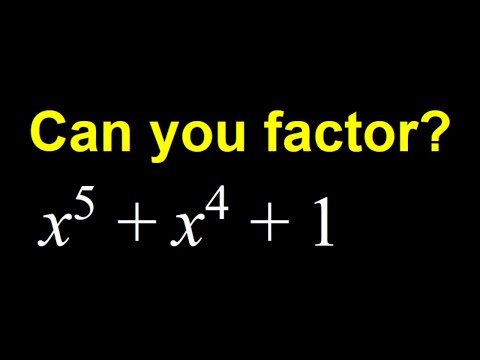 0:12:52
0:12:52
 0:01:01
0:01:01
 0:05:21
0:05:21
 0:04:34
0:04:34