filmov
tv
Factoring a Quintic | Challenging Algebra
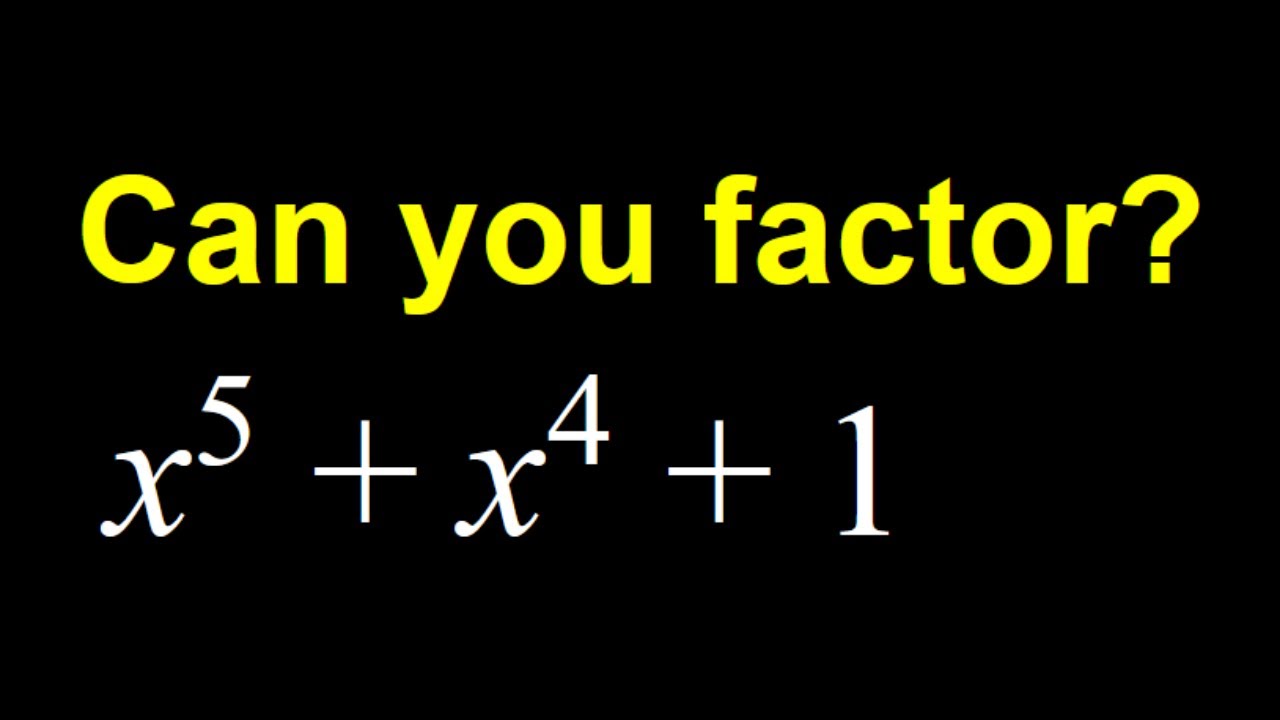
Показать описание
🤩 Hello everyone, I'm very excited to bring you a new channel (SyberMath Shorts)
Enjoy...and thank you for your support!!! 🧡🥰🎉🥳🧡
If you need to post a picture of your solution or idea:
#ChallengingMathProblems #PolynomialEquations #Polynomials
via @YouTube @Apple @Desmos @NotabilityApp @googledocs @canva
PLAYLISTS 🎵 :
Enjoy...and thank you for your support!!! 🧡🥰🎉🥳🧡
If you need to post a picture of your solution or idea:
#ChallengingMathProblems #PolynomialEquations #Polynomials
via @YouTube @Apple @Desmos @NotabilityApp @googledocs @canva
PLAYLISTS 🎵 :
Factoring a Quintic | Challenging Algebra
Factoring a Quintic | Challenging Algebra
Factoring x^5+x+1 | A Quintic
How To Factor Polynomials The Easy Way!
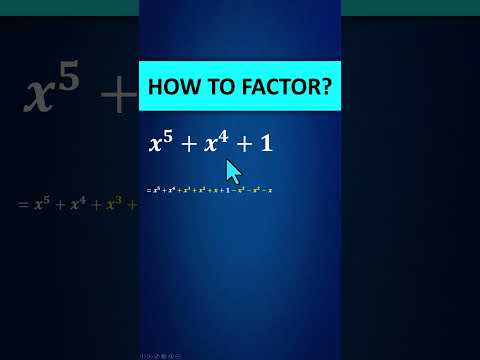
Can you factor this Quintic Polynomial | Factor of X^5 +X^4 + 1
Can you solve this cubic equation by factoring?
Factoring 5-term polynomials by grouping
Factoring A Quintic vol.2 | Polynomials #maths
Factoring a quintic sum
x^5+x^4+1 How to Factor Quintic Polynomial?
Factoring Cubic, Quartic, and Quintic Polynomials
Factoring A Quintic Trinominal #algebra #fast #mathematics #maths #shorts #challenge #equation
Factoring A Quintic | Polynomials #maths
Can You Factories A Quintic Trinomial in Just 40 Seconds? | #Shorts
Factor this quintic polynomial : x⁵+x⁴+1
Mastering Quintic Equation | Algebraic Challenge | Polynomials
How To Solve A Quintic Equation | Algebra | Math Olympiad
Solving Higher-Degree Polynomials by Synthetic Division and the Rational Roots Test
How To Factor Difficult Quadratic Equations
2 seconds trick to factorise cubic polynomial #mathtricks #fastcalculation
polynomials super trick to find roots of cubic equation | factorisation trick
Solving Polynomial Equations By Factoring and Using Synthetic Division
Factorising cubic functions: The kx method
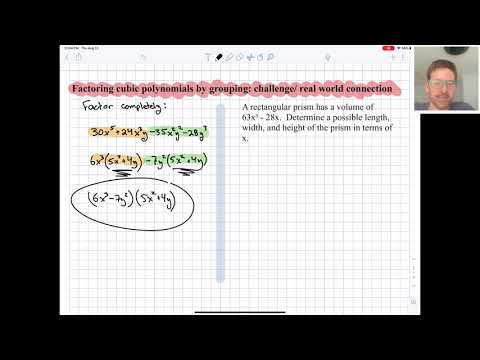
Algebra 1. Factoring cubic polynomials. Challenge, real world connection
Комментарии
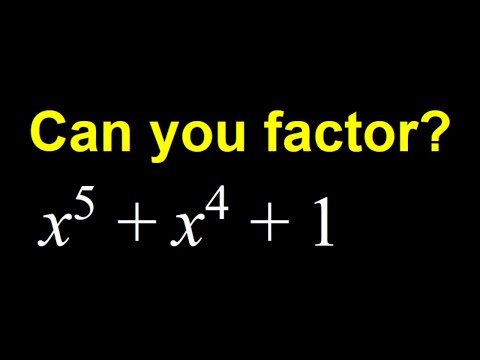 0:12:52
0:12:52
 0:12:52
0:12:52
 0:00:52
0:00:52
 0:11:54
0:11:54
 0:03:40
0:03:40
 0:00:59
0:00:59
 0:05:33
0:05:33
 0:02:08
0:02:08
 0:10:12
0:10:12
 0:00:54
0:00:54
 0:28:29
0:28:29
 0:00:27
0:00:27
 0:01:55
0:01:55
 0:00:55
0:00:55
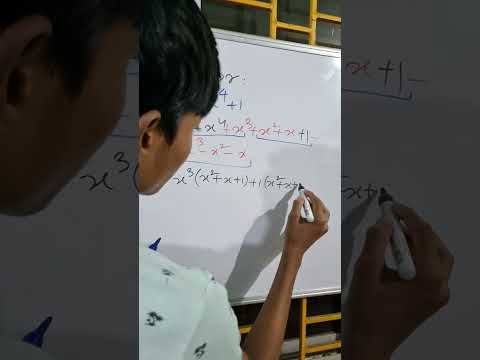 0:01:00
0:01:00
 0:08:52
0:08:52
 0:10:42
0:10:42
 0:09:22
0:09:22
 0:05:47
0:05:47
 0:00:30
0:00:30
 0:01:00
0:01:00
 0:14:19
0:14:19
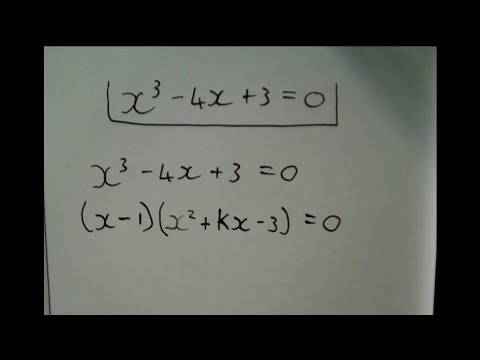 0:10:22
0:10:22
 0:04:16
0:04:16