filmov
tv
Factoring a cubic polynomial in two ways

Показать описание
This video is about factoring a cubic polynomial
If you need to post a picture of your solution or idea:
#ChallengingMathProblems #Polynomials
EXPLORE:
If you need to post a picture of your solution or idea:
#ChallengingMathProblems #Polynomials
EXPLORE:
How to factor a cubic function
He can factor a cubic trinomial
Factoring a Cubic Polynomial (Long Division)
Factoring a cubic polynomial in two ways
Factorising cubic functions: The kx method
How to factor a polynomial using the difference of two cubes
Can you solve this cubic equation by factoring?
Factoring 3x³ + x² - 15x - 5 #Shorts #algebra #math #maths #mathematics #education #learn #learning...
Factorise Cubic Equation Grade 12: Introduction
Factoring Cubic Trinomials
polynomials super trick to find roots of cubic equation | factorisation trick
Factorization of cubic polynomial in one minute |maths in short
How to factor a polynomial to the third degree by factoring out an x
Factor and Solve Cubic Equations in Less Than One Minute! - Super Simple Trick
Factoring a Cubic Polynomial - Algebra I
Factorising a Cubic Polynomial
Factorising Cubic Polynomials
FACTORIZE Cubic Equation Fast! #NVStyle
Factorise Cubic Equation Grade 12: Practice
How to Solve Advanced Cubic Equations: Step-by-Step Tutorial
Factoring a cubic polynomial by factoring out common terms first
Factoring a Cubic Polynomial (Synthetic Division 01)
Factoring Cubic Polynomials - Number Sense 101
Solving Polynomial Equations By Factoring and Using Synthetic Division
Комментарии
 0:04:45
0:04:45
 0:00:14
0:00:14
 0:08:58
0:08:58
 0:12:22
0:12:22
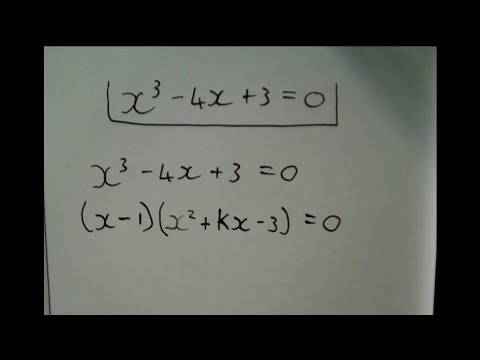 0:10:22
0:10:22
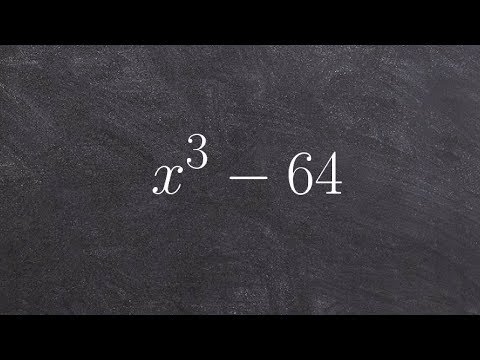 0:02:21
0:02:21
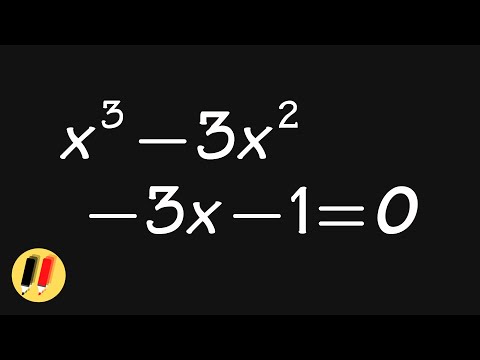 0:00:59
0:00:59
 0:00:47
0:00:47
 0:06:17
0:06:17
 0:07:15
0:07:15
 0:01:00
0:01:00
 0:01:00
0:01:00
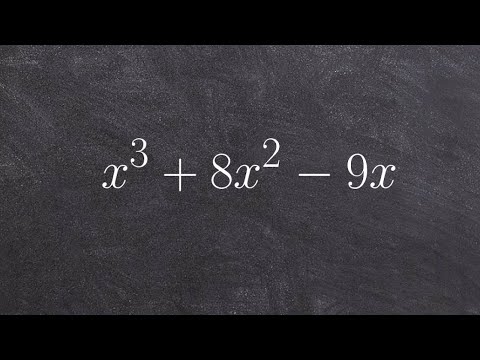 0:02:20
0:02:20
 0:07:18
0:07:18
 0:03:05
0:03:05
 0:01:00
0:01:00
 0:07:27
0:07:27
 0:01:00
0:01:00
 0:04:44
0:04:44
 0:10:52
0:10:52
 0:02:55
0:02:55
 0:03:56
0:03:56
 0:09:13
0:09:13
 0:14:19
0:14:19