filmov
tv
Intro Real Analysis, Lec 24: Convergence of Series, Geometric Series, p-Series Test, Divergence Test
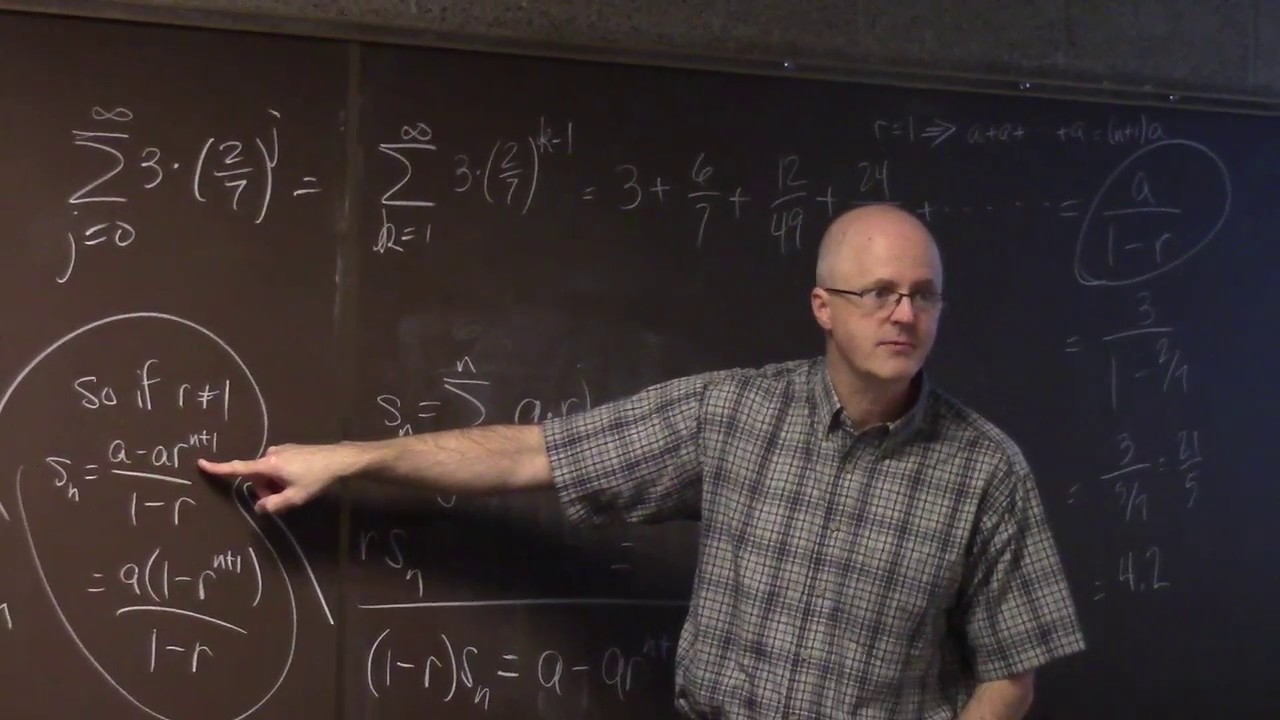
Показать описание
Introduction to Real Analysis, Lecture 24.
(0:00) Career night announcement. Exam 3 date and topic coverage.
(1:21) Definition of an infinite series (infinite sum) and what it means for an infinite series to converge (the series converges if and only if the corresponding sequence of partial sums converges).
(6:04) A convergent geometric series example. Be comfortable with both summation (sigma) notation and writing it out. Be able to identify the common ratio r. It sums to a/(1 - r), which for this example is 21/5 = 4.2.
(11:14) General derivation of the formula for the sum of a convergent geometric series (start by deriving the formula for the nth partial sum). The series converges if and only if r is strictly between -1 and 1.
(20:19) Definition of a p-series and a description of when they converge (when p is greater than 1) and diverge (when p is less than or equal to 1). When p = 1 it is the harmonic series. The harmonic series diverges by the integral test or by considering appropriate inequalities for special subsequences of the sequence of partial sums.
(30:11) Divergence test (If a series converges, then its terms must converge to zero. The contrapositive is: if the terms of a series do not converge to zero, then the series diverges). Make sure you distinguish between the sequence of terms and the sequence of partial sums.
(35:39) "Proof" that 0 = 1 (zero equals one proof).
(38:34) Cauchy criterion for convergence of an infinite series.
(42:32) For a series of non-negative terms, the series will converge if and only if its sequence of partial sums is bounded above (since the sequence of partial sums will be monotone increasing).
(46:13) Algebraic combinations (sums, differences, constant multiples) of convergent series are convergent (and converge to the corresponding algebraic combination of the sums of the original series). The proofs are related to corresponding properties of algebraic combinations of sequences.
Bill Kinney, Bethel University Department of Mathematics and Computer Science. St. Paul, MN.
AMAZON ASSOCIATE
As an Amazon Associate I earn from qualifying purchases.
0:53:40
Intro Real Analysis, Lec 24: Convergence of Series, Geometric Series, p-Series Test, Divergence Test
0:58:44
introduction to real analysis bartle solutions - Lec#24 Chapter#3 Exercise#3.1 Questions 1 to 5
0:49:56
introduction to real analysis bartle solutions - Lec#24(Part-2) Ch#3 Exercise#3.1 Questions 6 to 11
0:16:28
Lec-24 Power Series - Introduction and Convergence | Series of Functions
0:48:25
introduction to real analysis bartle solutions - Lec#24(Part-3) Ch#3 Exercise#3.1 Questions 12 to 18
0:10:05
Intro Real Analysis, (Rest of) Lec 14: Variation of a Function, Derivative Calculation Using Limits
0:33:53
Intro Real Analysis, Lec 16, Part 1: Mean Value Theorem: Statement, Basic Examples, and Proof
0:34:24
Intro Real Analysis, Lec 37, Part 2: Review Topology, Quick Review of Other Real Analysis Topics
0:10:34
Intro Real Analysis, Lec 19, Part 3: Review for Real Analysis Exam 2
0:58:40
Intro Real Analysis, Lec 35: Sup Norm and Metric on C[a,b], Sequence Space, Open & Closed Sets
0:57:48
Intro to Real Analysis, Lec 4: Cardinality, Cantor, Continuum Hypothesis, Ping Pong Ball Conundrum
0:09:53
How to self study pure math - a step-by-step guide
0:56:27
Intro Real Analysis, Lec 17: Mean Value Theorem Corollaries, Definition of Riemann Integral
0:56:35
Intro Real Analysis, Lec 12: Limits Involving Infinity, Continuity, Intermediate and Extreme Values
0:59:46
Intro Real Analysis, Lec 36: Chaos, Logistic Map, Period Doubling, Symbol Space, Shift Map
0:54:44
Intro Real Analysis, Lec 15: Uniform Continuity, Monotone Functions, Devil's Staircase, Derivat...
0:56:16
Intro Real Analysis, Lec 21: Convergence of Riemann Sums, Fundamental Theorem of Calculus
0:55:02
Intro Real Analysis, Lec 5: Archimedean Property of R, Cantor's Theorem, Sequences, Crazy Funct...
0:56:53
Intro Real Analysis, Lec 9: Recursive Sequences, Limit Superior & Inferior Definitions & Pro...
0:56:28
Intro Real Analysis, Lec 11: Continuity and the Intermediate Value Theorem (climbing Monk Story)
0:57:23
Intro Real Analysis, Lec 8: Subsequences, Bolzano-Weierstrass, Cauchy Criterion, Limsup & Liminf
0:20:54
Intro Real Analysis, Lec 16, Part 2: Summary of Corollaries of the Mean Value Theorem
0:45:59
introduction to real analysis bartle solutions - Lec#27 (Part-4) Ex#3.2 Q# 19 to 24 @Math Tutor 2
0:57:24
Intro Real Analysis, Lec 28: Taylor Series for sin(x), cos(x), e^(x), Uniform Convergence
Комментарии