Linear Algebra Derivation of Lorentz Transformation

Why the eigenvalues need to be positive:
We can write the vector (β,1) as a linear combination of the two eigenvectors. If one of the eigenvalues is negative, then (β,1) will get flipped along one of the axes of the eigenvectors. Because |β| is less than 1 we know that (β,1) starts out in the top region, above y=x and y=-x. Once it gets flipped it won't be in the top region anymore. In that case, it can't possibly equal (0,1) because (0,1) is in the top region. This contradicts our assumption. Therefore the eigenvalues can't be negative because that leads to a contradiction.
The eigenvalues also can't be zero because then there would be a nonzero null space, so the map would not be injective (multiple values map to zero), so it would not have an inverse. As a result, we know that the eigenvalues must be positive.

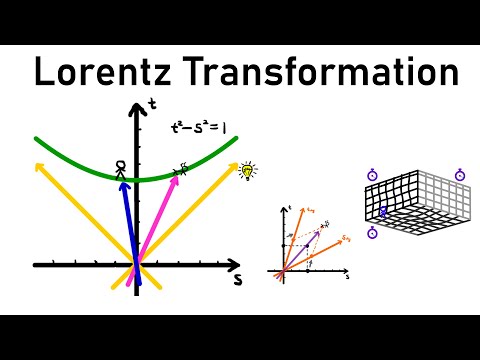
The Lorentz transformation is often derived using thought experiments about shooting light rays and things like that. But we can prove the matrix form of the Lorentz transformation in a more abstract way using linear algebra! This gives us a way to describe changes of coordinate system when we move between inertial reference frames.

0:00 Starting assumptions
6:20 Derivation

Subscribe to see more new math videos!

Music: C418 - Pr Department

[kiiometric]

Wow, I've always wondered how and why the Lorentz factor appeared in the time dilation equation, great video!

[Fysiker]

Thanks for the clear derivation, most satisfying one I've seen

[jamesbentonticer]

Thanks for putting the time of the actual derivation in the description. Appreciated :)

[x]

I am hopeful that you pursue an educating position at some point, maybe after passing physics with flying colors :D great video, and explained really well

[thomasolson]

γ=1/sqrt(1-(v/c)^2)

They look very similar, right? What about:

If cos is used, then what is sin?

I'm certain I've seen (v/c)*γ being used somewhere.
So we have cos and sin.

So, what we have is a complex number, but not yet. In this form we can find the radius by squaring. It is still, technically, a trig function.

Since it is a complex number, can't we just multiply by it's conjugate?
r:=7, v=3*c/4

That isn't the right answer is it? Well, the magnitude is (x+i*y)*(x-i*y). We need to multiply by i, even though it's already established to be a complex number.

So, there is this other identity that goes with this.
m/m_0=γ
The two work together, but I can't work with this as it is. I'm going to get them all on one side. This way the ratio can also be the radius.
1=γ*m_0/m
I am starting to see a problem here. If I treat m_0/m like it is the radius, it will be equal to 1.
(m_0/m)*γ+i*(m_0/m)*γ*v/c = 1+i*1*v/c= 1+i*v/c. || sqrt(1-(v/c)^2) || which is 1/γ = || m_0/m ||

1+i*v/c matches your form.
The series of arctan with the Lorentz Factor is also cool.
where -1 < v/c < 1
Which is actually, where -1 < y/x < 1

[NH-zhmp]

7:26 Could this method of eigenvector can be applied for the general case (Lorentz transformation in arbitrary direction) ?

[alejrandom]

10:54 fun fact, from this point we can notice that the matrix is isomorphic to split-complex numbers, and we can solve the rest in that system.

[coltonsowsun]

Finally I found the video I needed.... Thank you my friend for sharing your wisdom and experience with us! You deserve more views and subscribes.

[xcicada]

I took linear algebra during a break once on coursera just to get an idea of it because I was going to start a python/machine learning course. I remember half way through my linear algebra class I remembered a video I casually passed by regarding time dealation a long time ago and instantly drew the connection in how it's calculated. It was interesting for me, as someone who is not math savvy, because I was able to have an "aha!" moment of "so that's how they calculate crazy shi* like that!!"

[kevinowens]

Nicely done. Thank you for such a refreshing perspective.

[ohno]

Damn this is an incredible explanation, thanks for doing these

[jewulo]

But how is the Mathematics so capable of unentangling a fundamental property of Nature? That I find really perplexing. There is almost no Physics in your presentation but the presentation is about a fundamental property of Physics.

[CoolXstoffer]

Great video! Really clarified the derivation for me. I have a question regarding the measurement of t=1/c. Since time is a speed measured in m/s, woudn't it then be putting time = speed? I can't really grasp the intuition behind such a postulate, hence my comment. Thanks in advance, i love your videos!

[redaabakhti]

is the fact that the lorentz transform commute with reflections reflects (no pun I swear) the fact that reflections are a symmetry of the universe

[joeltovarramos]

Great video and it is very clear, thank you for make this content

[wuyqrbt]

Great as usual .
Thank you so much dear *Mu Prime* 💖

[datsmydab-minecraft-and-mo]

which physics and math courses have you taken? and are taking now? If you could do a topology series that would be great.

[robertflynn]

People don't know what a Lorentz transform is and why? Maybe write them out first in equations format

[alejrandom]

I always wondered why the LT matrix has determinant 1, now I see it has to do with the symmetry of being able to take the inverse by changing the sign of v

[Whoeveriam]

I have a question about the explanation of why the eigenvalues are positive in the description. We can write (β, 1) as a linear combination of two eigenvectors. But no matter how they are flipped around due to sign, they remain orthogonal and span the whole space. Thus you can also access the vectors in the region you want as well, so there is no contradiction