filmov
tv
Can you find the area of this triangle??
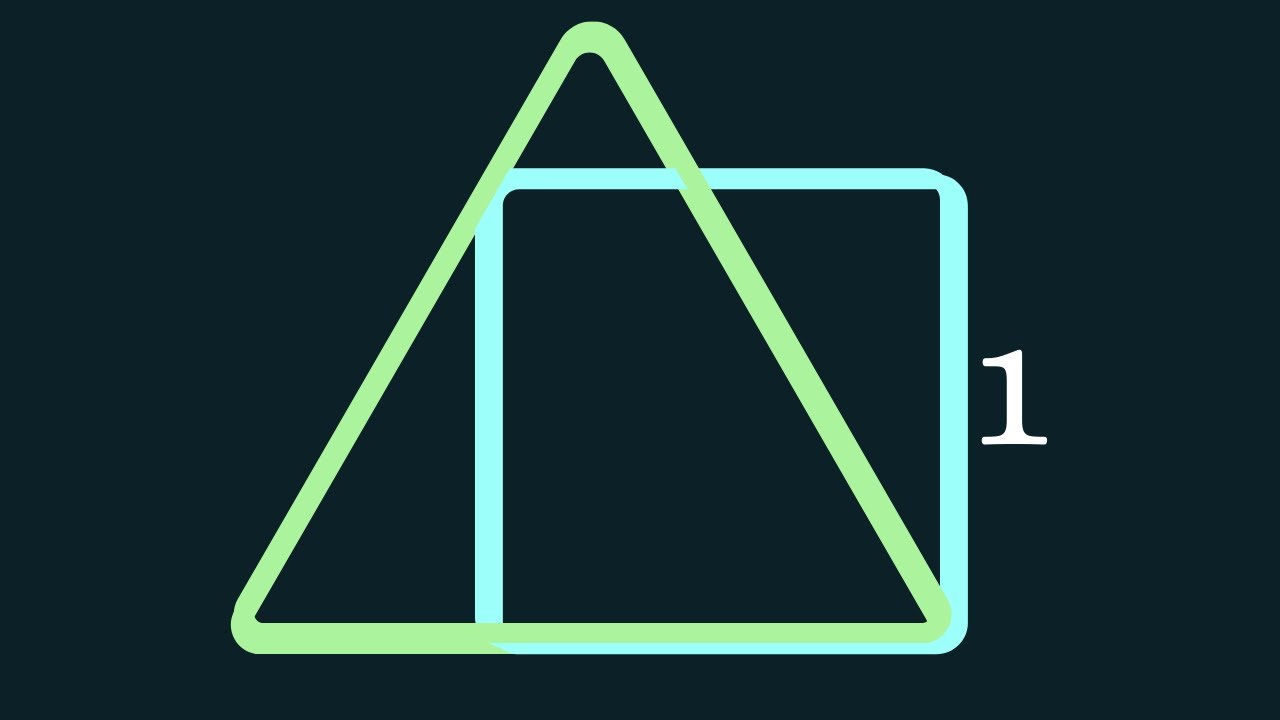
Показать описание
If you are going to use an ad-blocker, considering using brave and tipping me BAT!
Books I like:
Abstract Algebra:
Differential Forms:
Number Theory:
Analysis:
Calculus:
My Filming Equipment:
Math Antics - Area
Can you find the area of the right triangle? | (Algebra) | #math #maths | #geometry
[Request] how can we do that? Find the area of the square. Reddit geometry r/theydidthemath
Find the Area Challenge
Finding the Area of a Composite Figure | Area of Composite Rectangles
Can you find the area of the triangle? | (Perimeter) | #math #maths | #geometry
Can you find area of the Yellow shaded Trapezoid? | (Two Methods) | #math #maths | #geometry
Can You Find the Area of This Figure?
Can you find the area of shaded portion. #geometry #mathshorts
How to Find Area | Rectangles, Squares, Triangles, & Circles | Math Mr. J
Can you find area of the Green shaded region? | (Squares) | #math #maths | #geometry
How to Find the Area of a Square | Math with Mr. J
Can you find the area of the Purple triangle? | (Important Geometry skills explained) | #math #maths
Can you find the area of this triangle??
How to Find the Surface Area of a Rectangular Prism | Math with Mr. J
Area for Kids
Can you find area of the Yellow shaded Square? | (Triangle) | #math #maths | #geometry
Can you find area of the Green shaded triangle? | (Semicircle) | #math #maths #geometry
Can you find area of the Blue shaded Rectangle? | (Two Methods) | #math #maths | #geometry
How to Find the Area of a Rectangle | Math with Mr. J
Can you find area of the Yellow shaded Quarter circle? | (Square) | #math #maths | #geometry
No Calculators! | Can you find Area of the Yellow triangle? | #math #maths #geometry
Can you find area of the Yellow shaded region? | (Quarter Circle) | #math #maths | #geometry
Can You Find the Area of this Semicircle? | Step-by-Step Explanation
Комментарии
 0:10:26
0:10:26
 0:09:53
0:09:53
![[Request] how can](https://i.ytimg.com/vi/YAk0htu7FnQ/hqdefault.jpg) 0:03:56
0:03:56
 0:04:33
0:04:33
 0:07:14
0:07:14
 0:08:03
0:08:03
 0:11:48
0:11:48
 0:03:39
0:03:39
 0:00:48
0:00:48
 0:22:10
0:22:10
 0:08:52
0:08:52
 0:02:48
0:02:48
 0:11:19
0:11:19
 0:06:10
0:06:10
 0:04:57
0:04:57
 0:08:58
0:08:58
 0:08:42
0:08:42
 0:10:55
0:10:55
 0:09:59
0:09:59
 0:04:43
0:04:43
 0:09:04
0:09:04
 0:10:22
0:10:22
 0:12:43
0:12:43
 0:09:46
0:09:46