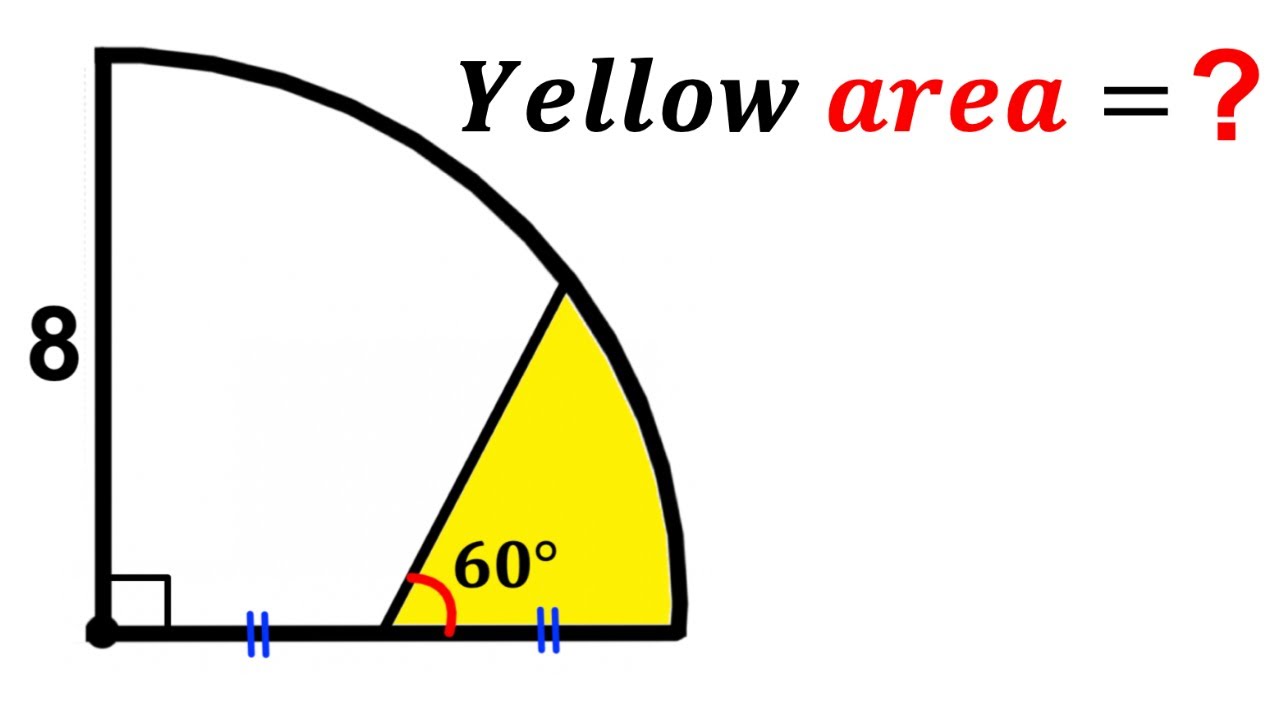
Can you find area of the Yellow shaded region? | (Quarter Circle) | #math #maths | #geometry

Today I will teach you tips and tricks to solve the given olympiad math question in a simple and easy way. Learn how to prepare for Math Olympiad fast!

Need help with solving this Math Olympiad Question? You're in the right place!

I have over 20 years of experience teaching Mathematics at American schools, colleges, and universities. Learn more about me at

Can you find area of the Yellow shaded region? | (Quarter Circle) | #math #maths | #geometry

Olympiad Mathematical Question! | Learn Tips how to solve Olympiad Question without hassle and anxiety!

#FindYellowArea #LawOfCosines #LawOfSines %QuadraticFormula #Triangle #GeometryMath #PythagoreanTheorem #AreaOfTriangle #IsoscelesTriangles
#MathOlympiad #CongruentTriangles #QuarterCircle
#OlympiadMathematicalQuestion #HowToSolveOlympiadQuestion #MathOlympiadQuestion #MathOlympiadQuestions #OlympiadQuestion #Olympiad #AlgebraReview #Algebra #Mathematics #Math #Maths #MathOlympiad #HarvardAdmissionQuestion
#MathOlympiadPreparation #LearntipstosolveOlympiadMathQuestionfast #OlympiadMathematicsCompetition #MathOlympics #ExteriorAngleTheorem #PythagoreanTheorem #IsoscelesTriangles #AreaOfTriangleFormula #AuxiliaryLines
#blackpenredpen #MathOlympiadTraining #Olympiad Question #GeometrySkills #GeometryFormulas #AreaOfTriangles #CompetitiveExams #CompetitiveExam
#MathematicalOlympiad #OlympiadMathematics #LinearFunction #TrigonometricRatios

How to solve Olympiad Mathematical Question
How to prepare for Math Olympiad
How to Solve Olympiad Question
How to Solve international math olympiad questions
international math olympiad questions and solutions
international math olympiad questions and answers
olympiad mathematics competition
blackpenredpen
Andy Math
math olympics
olympiad exam
olympiad exam sample papers
math olympiad sample questions
math olympiada
British Math Olympiad
olympics math
olympics mathematics
olympics math activities
olympics math competition
Math Olympiad Training
How to win the International Math Olympiad | Po-Shen Loh and Lex Fridman
Po-Shen Loh and Lex Fridman
Number Theory
There is a ridiculously easy way to solve this Olympiad qualifier problem
This U.S. Olympiad Coach Has a Unique Approach to Math
The Map of Mathematics
mathcounts
math at work
Pre Math
Olympiad Mathematics
Olympiad Question
Find Area of the Shaded Triangle
Geometry
Geometry math
Geometry skills
Right triangles
Exterior Angle Theorem
pythagorean theorem
Isosceles Triangles
Area of the Triangle Formula
Competitive exams
Competitive exam
Find Area of the Triangle without Trigonometry
Find Area of the Triangle
Auxiliary lines method
Pythagorean Theorem
Square
Diagonal
Congruent Triangles
coolmath
my maths
mathpapa
mymaths
cymath
sumdog
multiplication
ixl math
deltamath
reflex math
math genie
math way
math for fun

Subscribe Now as the ultimate shots of Math doses are on their way to fill your minds with the knowledge and wisdom once again.

[georgebliss]

8 /sin 120 = 4 / sin ODC.
Sin ODC = 4 x (sin 120) / 8 = 0.433.
ODC = 25.658 degrees.
COD = 180 - 120 - 25.658 = 34.342 degrees.
Area OCD = 1/2 x 8 x 4 x sin 34.342. = 9.026.
Area sector = Pi x 64 x 34.342 / 360 = 19.180.
Yellow area = 19.180 - 9.026 = 10.154.

[hongningsuen]

Method using sine law:
1. In triangle ODC, by sine law, sin(ODC)/4 = sin(120)/8.
sin(ODC) = (sqrt3)/4
Hence angle ODC = 25, 6589
2. In triangle ODC, angle COD = 60 - 25.6589 = 34.3411
3. Area of triangle ODC = (1/2)(8)(4)(sin34.3411) = 9.0259
4. Areaof sector OAD = (34.3411/360)(8)(8)(pi) = 19.1797
5. Area of yellow region = 19.1797 - 9.0259 = 10.1538

[marcgriselhubert]

Let's use an orthonormal center O, first axis (OA).
The equation of (CD) is y = tan(60°).(x - 4)
or y = sqrt(3).(x - 4)
The equation of the circle si x^2 + y^2 = 64
At the intersection D we have: x^2 + 3.(x - 4)^2 = 64
or 4.(x^4) - 24.x - 16 = 0, or x^4 - 6.x -4 = 0.
Deltaprime = 13, so x = 3 - sqrt(13) (rejected as negative)
or x = 3 + sqrt(13),
So D(3 + sqrt(13); sqrt(3).(-1 + sqrt(13)),
or D(3 +sqrt(3); sqrt(39) - sqrt(3))
Be t = angleAOD. tan(t) = (sqrt(39) -sqrt(3))/(3 +sqrt(13))
tan(t) = sqrt(3).(4 -sqrt(13)) (about 0.683)
Then t = Arctan(4.sqrt(3) -sqrt(39)). (about 0.6 rad or 34.3°)
The area of sectorAOD is (64.Pi).(t/(2.Pi)) =32.t
The area of triangle OCD is (1/2).OC.(ordinate of D)
so it is (1/2).(4).(sqrt(39) -sqrt(3)) = 2.(sqrt(39) - sqrt(3))
Finally the yellow area is:
32.Arctan(4.sqrt(3) -sqrt(39)) - 2.(sqrt(39) - sqrt(3))

[KipIngram]

Consider the triangle DOC. Length DO is 8, length OC is 4, and angle OCD is 120 degrees. By law of sines,

DO/sin(120) = 8/sin(120) = 4/sin(ODC) --> sin(ODC) = sin(120)/2

Now find angle DOC:

DOC = 180 - 120 - ODC
DOC = 60 - ODC
DOC = 60 - arcsin(sin(120)/2)
DOC = 34.3411 degrees

Now the y coordinate of D is 8*sin(34.3411) = 4.5129, and then length CD is found from 4.5129/CD = sin(60), CD = 4.5129/sin(60) = 5.2111. Now we can use Heron's formula to calculate the area of the triangle DOC:

p = (8 + 4 + 5.2111)/2 = 8.6056
area(DOC) = sqrt(p*(p-8)*(p-4)*(p-5.2111)
area(DOC) = 9.026

The area of the circle sector DOA is pi*8^2*34.3411/360 = 19.1797. Now the sought after area is just the sector area minus the triangle area:

Yellow_Area = 19.1797 - 9.026
Yellow_Area = 10.1532

Q.E.D.

[marioalb]

Sine rule, triangle COD:
sinβ / 4 = sin120°/ 8
β = 25, 6589°
Triangle COD:
α = 180° -120° - β
α = 34, 3411°
Angular sector AOD:
A = ½αR² = ½ α 8²
A = 19, 1797 cm²
Triangle COD:
A = ½ a b sinα = ½ 4 . 8. sinα
A = 9, 0259 cm²
Yellow shaded area:
A = A₁ - A₂
A = 10, 1538 cm² ( Solved √ )

[MarieAnne.]

That was pretty much the method I used, but I like to round at the end, so I got
Area = 32 arctan(√3(4−√13)) − 2√3(√13−1)) ≈ 10.15379

NOTE: Calculator has to be set to radians, and I used the following radian formula for sectors
A = πr² * α/(2π) = r²α/2

[alscents]

Seems quite complicated.
Choose origin at O = (0, 0)
Equation of Circle is
x^2 + y^2 = 8^2

C = (4, 0)
Equation of line CD is
(y - 0) = tan(60) (x - 4)
y = sqrt(3) (x - 4)

Assuming D = (a, b)
and substituting on line
b = sqrt(3) (a - 4)

and substituting in circle
a^2 + b^2 = 8^2
a^2 + (sqrt(3) (a - 4))^2 = 64
a^2 + 3 (a-4)^2 - 64 = 0
a^2+ 3 (a^2 - 8a + 16) - 64 = 0
a^2 + 3 a^2 - 24 a + 48 - 64 = 0
4 a^2 - 24 a - 16 = 0
a^2 - 6 a - 4 = 0
a = (6 +/- sqrt(36 + 16)) / (2 (1))
a = 3 +/- sqrt(13)
a = 3 + sqrt(13), after discarding negative value
b = sqrt(3)(3 + sqrt(13) - 4)
b = sqrt(39) - sqrt(3)

theta = angle(AOD)
cos(theta) = a / r = (3 + sqrt(13)) / 8
theta = arccos((3 + sqrt(13)) / 8)

Yellow Area = Area of sector AOD - Area of triangle COD
= pi r^2 (theta / 2 pi) - 4 b / 2
= pi 8^2 (theta / 2 pi) - 2 b
= 32 theta - 2 b
= 32 * arccos((3 + sqrt(13)) / 8) - 2 (sqrt(39) - sqrt(3))
= 32 * 0.599365154 - 2 * 4.51294719
= 10.15379 sq units

[johnbrennan]

Another way to do it is by finding angle odc .using sine rule and then you have angle doc. Then get the area

[johnryder]

Love the vid as usual, but at 7:43, should that not be a double inversion and the root 3 be multiplied by 8, not the 2 multiplied by it?

[quigonkenny]

As OA = r, OC = CA = r/2. As ∠DCA = 60°, ∠OCD = 180°-60° = 120°. By the law of cosines:

Triangle ∆OCD:
OD² = OC² + CD² - 2OC(CD)cos(120°)
r² = (r/2)² + CD² - 2(r/2)CD(-1/2)
r² = r²/4 + CD² + rCD/2
4r² = r² + 4CD² + 2rCD
4CD² + 2rCD - 3r² = 0
CD =
CD = -r/4 ± √(4r²+48r²)/8
CD = -r/4 ± √(52r²)/8
CD = -r/4 + √13r/4 --- CD > 0
CD = (√13-1)r/4

Drop a perpendicular from D to E on CA. Let ∠DOA = θ.

DE = CDsin(60°) = ((√13-1)r/4)(√3/2) = (√39-√3)r/8

sin(θ) = DE/OD = ((√39-√3)r/8)/r = (√39-√3)/8

The yellow shaded area is equal to the area of the sector subtended by minor arc DA minus the area of triangle ∆OCD:

Yellow shaded area DCA:
Aʏ = (θ/360°)πr² - r(r/2)sin(θ)/2
Aʏ = 64θπ/360 - 16((√39-√3)/8)
Aʏ = 8θπ/45 - 2(√39-√3)
Aʏ = 8πsin⁻¹((√39-√3)/8)/45 - 2√3(√13-1)
Aʏ ≈ 10.15 sq units

[AndreasPfizenmaier-yw]

If we draw a perpendicular from D to AC, is it possible to solve with a special triangle?

[prossvay]

Connect O to D
Angle OCD=180°-60°=120°
OC=AC=4
In ∆ OCD
Let CD=x

8^2=4^2+x^2-8x(-1/2)
So x=2√13-2

So COD=34.34°
Yellow square units.❤❤❤

[aljawad]

I used integral calculus to reach the same result. 👍🏼

[santiagoarosam]

"E" es la proyección ortogonal de D sobre OA y CE=a--->ED=a√3 ---> 8²-(4+a)²=(a√3)² ---> a=-1+√13---> tg(DOA)=a√3/(4+a) ---> <DOA=34, 34º ---> Área amarilla =(8²π*34, 34/360)-(4a√3/2) =10, 1532...
Gracias y saludos.
Esta solución es correcta. Incluyo paso intermedio omitido: Potencia de "E" respecto a la circunferencia =[8-(4+a)]*[8+(4+a)] =8²-(4+a)² =(a√3)²

[wackojacko]

First we had 2 sides and an angle. Apply Law of Cosines. Next we have 2 sides and an angle and need to find a missing angle. Apply Law of Sines. Find Sector area. Next find area of Triangle OCD. Use calculator! 🙂 ...cue some Mariachi music and tiptoe thru the tulips with a little bit of subtraction and wallah, problem solved! 🙂

[unknownidentity]

Let's find the area:
.
..
...
....


Let's assume that O is the center of the coordinate system and that OA and OB are located on the x-axis and y-axis, respectively. Then we obtain the following coordinates from the sketch:

O: ( 0 ; 0 )
A: ( 8 ; 0 )
B: ( 0 ; 8 )
C: ( 4 ; 0 )
D: ( xD ; yD )

The line CD is represented by the following function:

y = [(yD − yC)/(xD − xC)]*(x − xC) + yC = tan(60°)*(x − 4) + 0 = √3*(x − 4)

Since D is located on the quarter circle, the coordinates of D can be calculated in the following way:

xD² + yD² = R² = 8² = 64
xD² + 3*(xD − 4)² = 64
xD² + 3*xD² − 24*xD + 48 = 64
4*xD² − 24*xD − 16 = 0
xD² − 6*xD − 4 = 0

xD = 3 ± √(3² + 4) = 3 ± √(9 + 4) = 3 ± √13

Since xD>0, the only useful solution is:

xD = 3 + √13
yD = √3*(xD − 4) = √3*(3 + √13 − 4) = √3*(√13 − 1)

tan(∠AOD) = tan(∠COD)
= yD/xD
= √3*(√13 − 1)/(√13 + 3)
= √3*(√13 − 1)(√13 − 3)/[(√13 + 3)(√13 − 3)]
= √3*(13 − 4√13 + 3)/(13 − 9)
= √3*(16 − 4√13)/4
= √3*(4 − √13)

sin(∠AOD) = sin(∠COD) = yD/R = √3*(√13 − 1)/8

Now we are able to calculate the area of the yellow region:

A(yellow)
= A(circle sector OAD) − A(triangle OCD)
= πR²*[∠AOD/(2π)] − (1/2)*OC*OD*sin(∠COD)
= R²*arctan(yD/xD)/2 − (1/2)*(R/2)*R*sin(∠COD)
= 8²*arctan[√3*(4 − √13)]/2 − (1/2)*(8/2)*8*[√3*(√13 − 1)/8]
= 32*arctan[√3*(4 − √13)] − 2√3*(√13 − 1)
≈ 10.15

Best regards from Germany

[hervechampagne]

Once you e have calculated the value of x, isn't it easier to calculate the area of a circle whom radius is X (2(-1+sqare root of 13) and next divide it by six ? Because the angle of CDA is 60° ?

[juanalfaro]

Yellow Area = [DOA circle wedge] - [DOC]. Let DC=X, then 8^2 = 4^2 + X^2 - 2*4*X*cos (120) -> 64 = 16 + X^2 + 4x -> X^2 - 4X - 48 = 0 -> X^2-4X+4 = (X+2) ^2 = 52 -> X+2 = 2*sqrt (13) -> X = 2sqrt (13) - 2 = 2*[sqrt (13) - 1]. Find [DOC]: X/sin (DOC) = 8/sin (120) -> sin (DOC) = X*sin (120)/8 = 2*[sqrt (13)-1] * (sqrt (3)/2)/8 = [sqrt (39) - sqrt (3)]/8 -> DOC=34.3411. Now Yellow Area = (DOC/360) * Pi*R^2 - 8*4/2 * sin (DOC) = [(34.3411/360) * 64*Pi] - [16*sin (34.3411)] = 19.1797 - 9.0259 = 10.1538 sq. units

[giuseppemalaguti]

CD=a..DOC=α R=8 ..legge del Ayellow=32arcsin((√39-√3)/8)-2(√39-√3)=10, 154....

[ibajobadmission]

I am Bangladeshi student. We are facing a dangerous situation.