filmov
tv
Find the Area Challenge

Показать описание
Presh Talwalkar has a neat shortcut in this video.
Find the Area Challenge
Find the AREA challenge! One Circle In Another - Concentric Circles - Cool Geometry Problem
Find the Red Area Area
Tricky Geometry Challenge
Area of this Rectangle
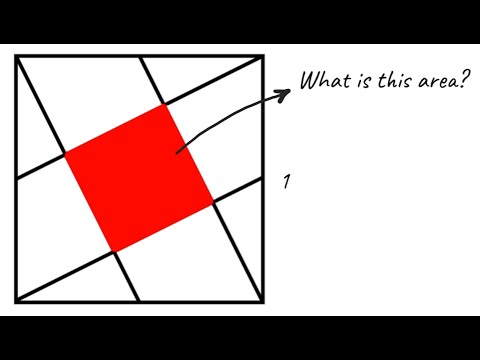
Multicolor Square Problem
2 Circles 1 Square
Area of Red Triangle
How To Solve For The Area - Viral Math Problem
Can You Find the Area of this Triangle | Geometry Challenge!
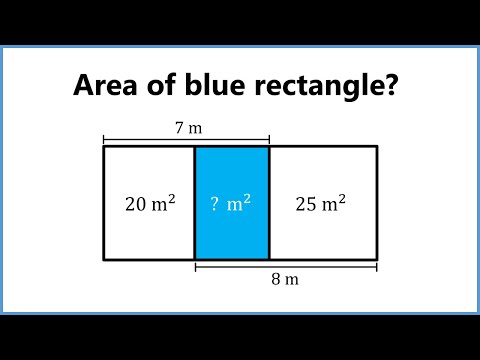
Find the area of the middle rectangle
Finding the Area of a Composite Figure | Area of Composite Rectangles
What Is The Area? Challenge From Croatia
Can You Find Angle X? | Geometry Challenge!
Genius student solved this in 1 minute - insanely hard geometry problem
Do you know Leonardo da Vinci's circle area proof?
Trig challenge problem: area of a hexagon | Math for fun and glory | Khan Academy
3rd Grade Perimeter & Area of Irregular Figures
Find Area of the Shaded Triangle in a Rectangle | Important Geometry skills explained | Fun Olympiad
7-Day Face Yoga Challenge!The result surprised me!
How to Measure Square Feet
How to Find the Area of a Triangle Using Trigonometry
Area Mastery: Tackle this Math Olympiad Challenge and Discover the Solution
Guess The Country on The Map - EUROPE | Geography Quiz Challenge
Комментарии
 0:04:33
0:04:33
 0:03:36
0:03:36
 0:01:40
0:01:40
 0:02:54
0:02:54
 0:01:56
0:01:56
 0:02:33
0:02:33
 0:03:35
0:03:35
 0:02:07
0:02:07
 0:05:48
0:05:48
 0:03:09
0:03:09
 0:03:25
0:03:25
 0:07:14
0:07:14
 0:05:55
0:05:55
 0:08:44
0:08:44
 0:09:24
0:09:24
 0:00:54
0:00:54
 0:18:18
0:18:18
 0:12:29
0:12:29
 0:10:37
0:10:37
 0:00:17
0:00:17
 0:00:24
0:00:24
 0:05:04
0:05:04
 0:08:03
0:08:03
 0:12:48
0:12:48