filmov
tv
Power sums with Calculus.

Показать описание
🌟Support the channel🌟
🌟my other channels🌟
🌟My Links🌟
🌟How I make Thumbnails🌟
🌟Suggest a problem🌟
🌟my other channels🌟
🌟My Links🌟
🌟How I make Thumbnails🌟
🌟Suggest a problem🌟
Power sums with Calculus.
Power sum MASTER CLASS: How to sum quadrillions of powers ... by hand! (Euler-Maclaurin formula)
Summation Formulas and Sigma Notation - Calculus
Summing powers of 1/8 visually!
General Method for Integer Power Sum Formula
Finding the Sum of a Series by Differentiating
Power Series
Math Integration Timelapse | Real-life Application of Calculus #math #maths #justicethetutor
Representation of Boolean Functions : SOP, POS || Digital Design || Himanshu Agarwal
Geometry of sums of powers of 1/5
Riemann Sums - Left Endpoints and Right Endpoints
Every Student Should See This
when calculus students use trig identities too early
Finding Power Series By Differentiation
Finding The Sum of an Infinite Geometric Series
Summation and Sums of Powers | Algebraic Calculus One | Wild Egg
Integration (Calculus)
How to Find a Definite Integral using Riemann Sums and the Limit Definition: Quadratic Example
Power Series - Representation of Functions - Calculus 2
an excruciatingly deep dive into the power sum.
How to Shift the Index of Summation with Infinite Series
what is sigma notation and how to we use it
Power Series - Differentiation and Integration - Calculus 2
Convergence and Divergence - Introduction to Series
Комментарии
 0:17:20
0:17:20
 0:50:01
0:50:01
 0:20:24
0:20:24
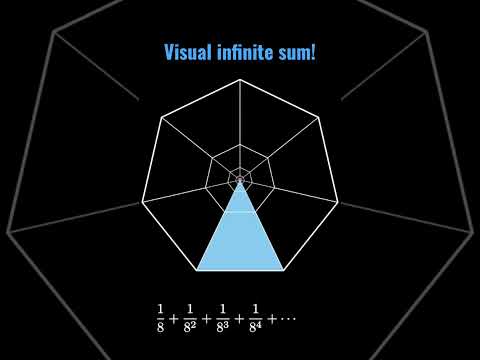 0:00:53
0:00:53
 0:06:06
0:06:06
 0:04:01
0:04:01
 0:06:48
0:06:48
 0:00:09
0:00:09
 0:39:52
0:39:52
 0:00:53
0:00:53
 0:20:10
0:20:10
 0:00:58
0:00:58
 0:00:43
0:00:43
 0:20:41
0:20:41
 0:19:50
0:19:50
 0:24:07
0:24:07
 0:07:04
0:07:04
 0:13:18
0:13:18
 0:53:45
0:53:45
 0:16:45
0:16:45
 0:06:10
0:06:10
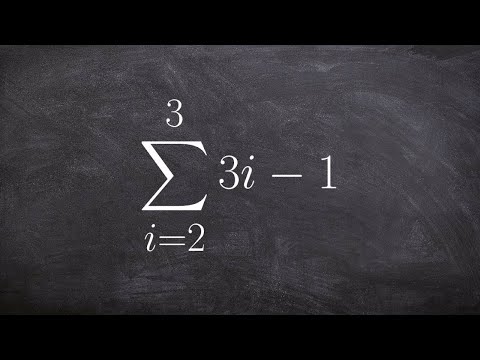 0:01:22
0:01:22
 0:34:36
0:34:36
 0:16:18
0:16:18