filmov
tv
when calculus students use trig identities too early

Показать описание
#shorts #funny #sad #calculus #studentlife
-----------------------------------------------------
------------------------------------------------------------------------------------
bprp #fast #funny #sad
when calculus students use trig identities too early
The Best Way to Master Trigonometric Identities
And You Thought Trigonometry Was Pointless…
Trigonometry - The signs of trigonometric functions
Trigonometry is wasy
What Integration Technique Should I Use? (trig sub, u sub, DI method, partial fractions) calculus 2
🤯 This ONE CIRCLE will make you finally understand trigonometry #shorts
Calculus of Trigonometric Functions (1 of 3: Using visual intuition)
Trigonometric ratios #maths #algebra #trigonometry #school #education #study #fyp #shorts #students
Calculus 2: Integration - Trig Substitution (1 of 28) What Is & When to Use Trig Substitution?
Integration By Trigonometric Substitution
Trigonometry For Beginners!
Trig Identities
Trigonometry Concepts - Don't Memorize! Visualize!
Trigonometry made easy
Limits of Trigonometric Functions | Calculus Tutorial
Why is Trigonometry so important?
Trig is fun
GCSE Maths - All the Trigonometry Equations you Need To know! #119
trig integrals involving sine and cosine (calculus 2)
#Trigonometry all formulas
Length of Shortest Ladder over a Fence Trigonometric Optimisation Calculus
Calculus 2 Lecture 7.2: Techniques For Trigonometric Integrals
The Hardest Math Test
Комментарии
 0:00:43
0:00:43
 0:03:36
0:03:36
 0:01:00
0:01:00
 0:06:13
0:06:13
 0:00:12
0:00:12
 0:22:40
0:22:40
 0:01:00
0:01:00
 0:07:38
0:07:38
 0:01:01
0:01:01
 0:02:58
0:02:58
 0:15:55
0:15:55
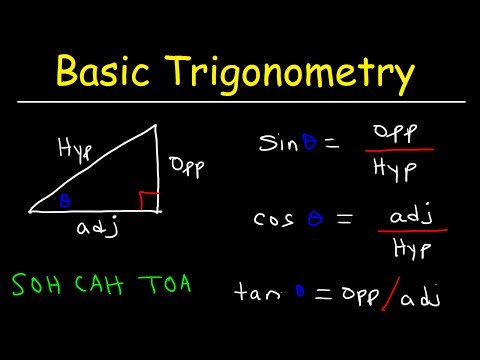 0:21:52
0:21:52
 0:27:57
0:27:57
 0:32:35
0:32:35
 0:12:43
0:12:43
 0:00:31
0:00:31
 0:05:20
0:05:20
 0:00:30
0:00:30
 0:02:53
0:02:53
 0:15:42
0:15:42
 0:00:16
0:00:16
 0:10:23
0:10:23
 2:21:10
2:21:10
 0:00:28
0:00:28