filmov
tv
Complex number fundamentals | Ep. 3 Lockdown live math

Показать описание
Intro to the geometry complex numbers.
Beautiful pictorial summary by @ThuyNganVu:
Errors:
- On the first sketch of a complex plane, there is a "2i" written instead of "-2i".
- At the end, in writing the angle sum identity, the last term should be sin(beta) instead of sin(alpha).
- During Q9, the terms in parentheses should include an i, (1/2 + sqrt(3)/2 i)
Thanks to these viewers for their contributions to translations
Hebrew: Omer Tuchfeld
------------------
The live question setup with stats on-screen is powered by Itempool.
The graphing calculator used here is Desmos.
The "Complex slide rule" came from Geogebra, via Ben Sparks.
Curious about other animations?
Music by Vincent Rubinetti.
Download the music on Bandcamp:
Stream the music on Spotify:
If you want to contribute translated subtitles or to help review those that have already been made by others and need approval, you can click the gear icon in the video and go to subtitles/cc, then "add subtitles/cc". I really appreciate those who do this, as it helps make the lessons accessible to more people.
------------------
Video Timeline (thanks to user "Just TIEriffic")
0:00:30 - W3 Results
0:01:00 - W4 Prompt
0:02:00 - Ask What would you call 'imaginary numbers'?
0:06:40 - Startingpoint & assumptions
0:10:25 - W4 Results
0:11:25 - Q1 Prompt
0:12:20 - Q1 Process
0:14:05 - RotatingCoordinates
0:16:40 - Q1 Result
0:17:40 - Q2
0:18:15 - Q3 Prompt
0:19:40 - Q3 Results
0:21:35 - RotationAnimation
0:22:35 - 3 facts about Multiplication
0:25:40 - Q4 Prompt
0:26:10 - Ask imaginary I vs physics i&j
0:28:15 - Q4 Result
0:31:00 - GeoGebraDemo
0:32:10 - Q5 Prompt
0:33:30 - Q5 Results
0:34:00 - Q5 Solution
0:35:55 - RotatingImages Example
0:37:10 - PythonExample
0:38:25 - PythonImage Rotation Example
0:40:35 - Ask Vectors & Matrices for rotation
0:42:40 - Q6 Prompt
0:46:55 - Q6 Results
0:47:25 - Q6 Solution
0:52:20 - RedefiningAngle Addition
0:57:20 - Q7 Prompt
0:57:55 - Ask Can we do without complex numbers?
1:00:10 - Q7 Results
1:00:55 - Q7 Solution
1:05:45 - Q8 Prompt
1:06:30 - Ask sum/difference of angles
1:09:25 - Q8 Results
1:10:25 - Q8 Solution
1:12:00 - DesmosExample
1:15:05 - Bringing it all together
1:16:25 - The "cis" shorthand explained
1:18:05 - Q9 Prompt
1:19:35 - Q9 Results
1:20:55 - ClosingRemarks
------------------
Various social media stuffs:
Beautiful pictorial summary by @ThuyNganVu:
Errors:
- On the first sketch of a complex plane, there is a "2i" written instead of "-2i".
- At the end, in writing the angle sum identity, the last term should be sin(beta) instead of sin(alpha).
- During Q9, the terms in parentheses should include an i, (1/2 + sqrt(3)/2 i)
Thanks to these viewers for their contributions to translations
Hebrew: Omer Tuchfeld
------------------
The live question setup with stats on-screen is powered by Itempool.
The graphing calculator used here is Desmos.
The "Complex slide rule" came from Geogebra, via Ben Sparks.
Curious about other animations?
Music by Vincent Rubinetti.
Download the music on Bandcamp:
Stream the music on Spotify:
If you want to contribute translated subtitles or to help review those that have already been made by others and need approval, you can click the gear icon in the video and go to subtitles/cc, then "add subtitles/cc". I really appreciate those who do this, as it helps make the lessons accessible to more people.
------------------
Video Timeline (thanks to user "Just TIEriffic")
0:00:30 - W3 Results
0:01:00 - W4 Prompt
0:02:00 - Ask What would you call 'imaginary numbers'?
0:06:40 - Startingpoint & assumptions
0:10:25 - W4 Results
0:11:25 - Q1 Prompt
0:12:20 - Q1 Process
0:14:05 - RotatingCoordinates
0:16:40 - Q1 Result
0:17:40 - Q2
0:18:15 - Q3 Prompt
0:19:40 - Q3 Results
0:21:35 - RotationAnimation
0:22:35 - 3 facts about Multiplication
0:25:40 - Q4 Prompt
0:26:10 - Ask imaginary I vs physics i&j
0:28:15 - Q4 Result
0:31:00 - GeoGebraDemo
0:32:10 - Q5 Prompt
0:33:30 - Q5 Results
0:34:00 - Q5 Solution
0:35:55 - RotatingImages Example
0:37:10 - PythonExample
0:38:25 - PythonImage Rotation Example
0:40:35 - Ask Vectors & Matrices for rotation
0:42:40 - Q6 Prompt
0:46:55 - Q6 Results
0:47:25 - Q6 Solution
0:52:20 - RedefiningAngle Addition
0:57:20 - Q7 Prompt
0:57:55 - Ask Can we do without complex numbers?
1:00:10 - Q7 Results
1:00:55 - Q7 Solution
1:05:45 - Q8 Prompt
1:06:30 - Ask sum/difference of angles
1:09:25 - Q8 Results
1:10:25 - Q8 Solution
1:12:00 - DesmosExample
1:15:05 - Bringing it all together
1:16:25 - The "cis" shorthand explained
1:18:05 - Q9 Prompt
1:19:35 - Q9 Results
1:20:55 - ClosingRemarks
------------------
Various social media stuffs:
Комментарии
 1:22:11
1:22:11
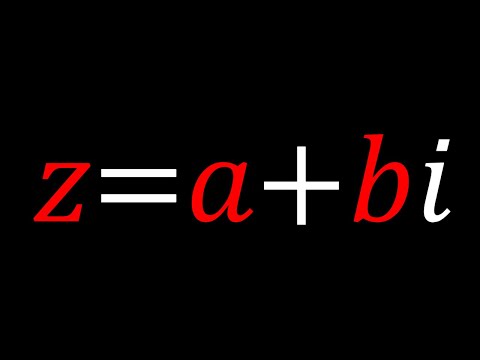 0:10:58
0:10:58
 0:09:40
0:09:40
 0:11:05
0:11:05
 0:08:37
0:08:37
 0:08:07
0:08:07
 0:08:55
0:08:55
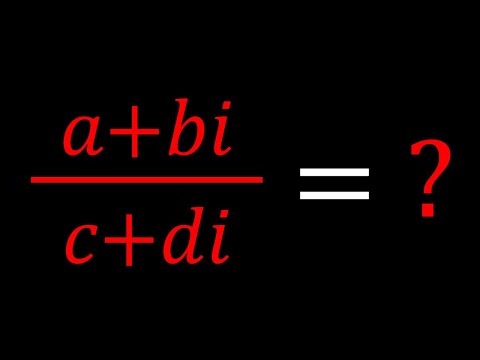 0:08:50
0:08:50
 0:59:53
0:59:53
 0:07:39
0:07:39
 0:09:34
0:09:34
 0:09:06
0:09:06
 1:13:17
1:13:17
 0:32:11
0:32:11
 0:03:22
0:03:22
 0:14:12
0:14:12
 0:50:04
0:50:04
 0:04:08
0:04:08
 0:51:16
0:51:16
 0:11:12
0:11:12
 0:13:42
0:13:42
 0:03:55
0:03:55
 0:23:29
0:23:29
 0:09:02
0:09:02