filmov
tv
Linear Algebra - Lecture 10 - Homogeneous Linear Systems

Показать описание
In this lecture, we define "homogeneous" linear systems, and discuss how to find the solutions to these systems in parametric vector form.
Linear Algebra - Lecture 10 - Homogeneous Linear Systems
Gaussian elimination | Lecture 10 | Matrix Algebra for Engineers
Algebra Lecture 10 pt 1 : Inner Product + Eigen Value/Vector . Dr / Ahmed Essam .
Gilbert Strang: Linear Algebra vs Calculus
Linear transformations | Matrix transformations | Linear Algebra | Khan Academy
Gil Strang's Final 18.06 Linear Algebra Lecture
Which of the following are Subspaces | Examples Proved | Linear Algebra | (Lecture 10)
Linear combinations, span, and basis vectors | Chapter 2, Essence of linear algebra
10th Class Mathematics, Chapter 1, Exercise 1.1, Question 3, Part 10 | MATH@m.imathematics
Cross products | Chapter 10, Essence of linear algebra
Linear Algebra II: Oxford Mathematics 1st Year Student Lecture - James Maynard
Linear Algebra - Matrix Operations
10th Algebra Chapter 1 | Practice Set-1.5 | Linear Equations in Two Variables | Lecture 10 |
Vectors | Chapter 1, Essence of linear algebra
Eigenvectors and eigenvalues | Chapter 14, Essence of linear algebra
Linear transformations and matrices | Chapter 3, Essence of linear algebra
Nonlinear algebra, Lecture 10: 'Invariant Theory', by Bernd Sturmfels
Linear Algebra - Lecture 7 - Linear Combinations and Vector Equations
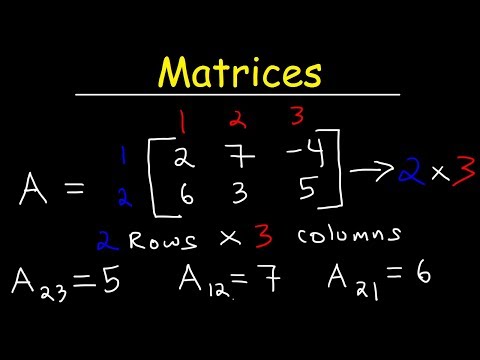
Intro to Matrices
Solve a System of Linear Equations Using LU Decomposition
Row Echelon Form of the Matrix Explained | Linear Algebra
Linear Algebra - Lecture 28 - Subspaces
Intro: A New Way to Start Linear Algebra
Linear Algebra - Lecture 27 - Vector Spaces
Комментарии
 0:08:54
0:08:54
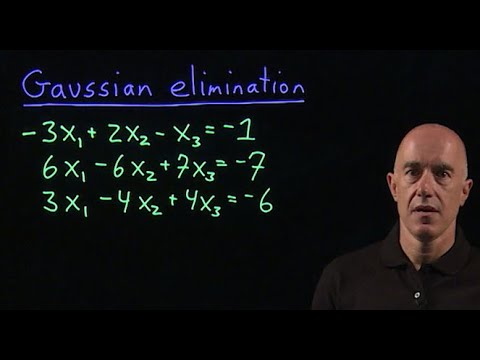 0:14:00
0:14:00
 1:17:21
1:17:21
 0:02:14
0:02:14
 0:13:52
0:13:52
 1:05:09
1:05:09
 0:18:21
0:18:21
 0:09:59
0:09:59
 0:00:52
0:00:52
 0:08:54
0:08:54
 0:53:55
0:53:55
 0:07:08
0:07:08
 0:34:49
0:34:49
 0:09:52
0:09:52
 0:17:16
0:17:16
 0:10:59
0:10:59
 1:48:16
1:48:16
 0:08:10
0:08:10
 0:11:23
0:11:23
 0:08:23
0:08:23
 0:11:11
0:11:11
 0:10:58
0:10:58
 0:04:15
0:04:15
 0:08:02
0:08:02