filmov
tv
How I wish logistic growth was taught to me in Calc 2

Показать описание
►Follow me
Join this channel to get access to perks:
►My Setup:
Join this channel to get access to perks:
►My Setup:
How I wish logistic growth was taught to me in Calc 2
Logistic Growth Model | The Westcoast Math Tutor
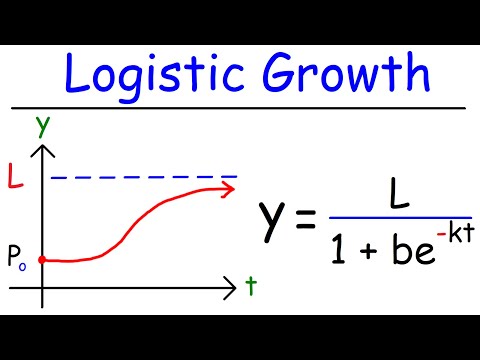
Logistic Growth
Simulating Competition and Logistic Growth
Logistic Growth Function and Differential Equations
Logistic growth model of a population (KristaKingMath)
logistic growth 1
logistic growth functions (for precalculus)
Excel Solver Demo: Fitting Data to Logistic Growth Model -- AIDS Deaths
Population Growth Models- Exponential, Logistic... Explained!
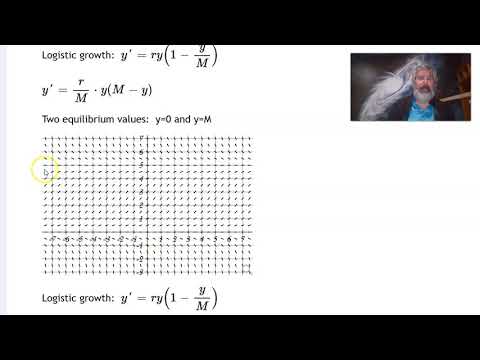
Logistic Growth
Logistic Growth - Population Example
4.8 Logistic Growth Functions
Modelling Population Growth with the Logistic Model: IVP
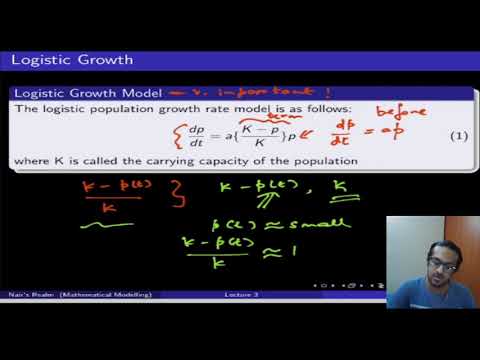
Logistic Growth Model
Python Scipy Demo: Nonlinear Fit of AIDS data to Logistic Growth Model
Ex: Logistic Growth Differential Equation
8 5 NOTES Logistic Growth
Logistic Differential Equation (general solution)
Solving A Logistic Growth Word Problem: Step-by-Step Tutorial (Precalculus)
Logistic Growth - Differential Equations in Action
Example 6 4 6 Logistic growth trendline
Mathematical Modelling - The Logistic Population Growth Model
Exponential v. Logistic Growth
Комментарии
 0:08:49
0:08:49
 0:05:26
0:05:26
 0:10:56
0:10:56
 0:07:30
0:07:30
 0:43:07
0:43:07
 0:06:26
0:06:26
 0:20:09
0:20:09
 0:09:47
0:09:47
 0:11:54
0:11:54
 0:03:15
0:03:15
 0:14:33
0:14:33
 0:07:04
0:07:04
 0:09:04
0:09:04
 0:07:00
0:07:00
 0:06:48
0:06:48
 0:13:37
0:13:37
 0:07:11
0:07:11
 0:43:58
0:43:58
 0:10:52
0:10:52
 0:03:18
0:03:18
 0:01:20
0:01:20
 0:02:21
0:02:21
 0:20:15
0:20:15
 0:03:44
0:03:44