filmov
tv
Differential Equations - 11 - Modeling with 1st Order Diff. Eq's (Tank Problem)

Показать описание
Demonstrating how to model a system with a 1st order differential equation with a Tank Problem.
Existence and Uniqueness of Solutions (Differential Equations 11)
Differential Equations - 11 - Modeling with 1st Order Diff. Eq's (Tank Problem)
Calculus 2: Modeling with Differential Equations (Video #11) | Math with Professor V
Edexcel A level Maths: 11.10 Solving Differential Equations (Part 1)
11 - Solve Differential Equations (ODEs) w/ Laplace Transforms, Part 3
The principle of superposition | Lecture 11 | Differential Equations for Engineers
Difference Between Partial and Total Derivative
Integration 24 • Differential Equations • P2 Ex11J • 🎲
CSIR NET DEC 2024 | Mathematical Science | ODE | PYQs For GATE Exam | By Raman Sir
🔵11 - Homogeneous First Order Differential Equations (Solved Examples)
the differential equations terms you need to know.
Solving Differential Equations(ODEs) in Mathematica | Tutorial -11
How to determine the general solution to a differential equation
Mixing Salt and Water - First Order Differential Equations
Integration (11) - Differential Equations (C4 Maths A-Level)
Session 11: Laplace transform to solve differential equations if INITIAL condition is NOT given at 0
Separable First-Order Differential Equations ~ Calculus 2
Differential Equations L-11 | CBSE Class 12 Maths | Class 12 Board Sprint | Arvind Sir | Vedantu JEE
Newton's Law of Cooling | First order differential equations | Khan Academy
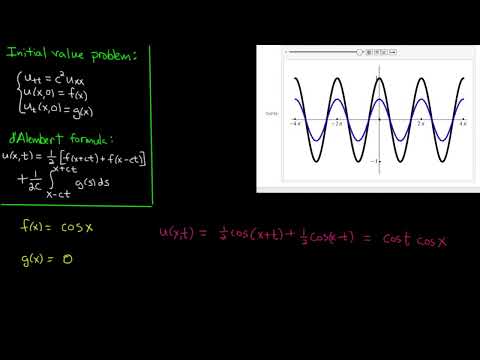
Partial Differential Equations 11: Wave equation, d'Alembert examples
Differential Equations Book for Beginners
Order And Degree Of Differential Equations | Differential Equation Class 12
Power Series Solutions of Differential Equations
Newton's Law of Cooling Calculus, Example Problems, Differential Equations
Комментарии
 0:44:32
0:44:32
 0:10:15
0:10:15
 0:16:00
0:16:00
 0:14:07
0:14:07
 0:27:31
0:27:31
 0:06:37
0:06:37
 0:01:44
0:01:44
 0:23:53
0:23:53
 0:37:46
0:37:46
 0:42:58
0:42:58
 0:01:00
0:01:00
 0:09:14
0:09:14
 0:02:03
0:02:03
 0:11:49
0:11:49
 0:22:17
0:22:17
 0:12:37
0:12:37
 0:12:01
0:12:01
 1:04:53
1:04:53
 0:10:01
0:10:01
 0:14:31
0:14:31
 0:00:25
0:00:25
 0:01:55
0:01:55
 0:11:45
0:11:45
 0:23:06
0:23:06