filmov
tv
Existence and Uniqueness of Solutions (Differential Equations 11)

Показать описание
THIS VIDEO CAN SEEM VERY DECEIVING REGARDING CONTINUITY. As I watched this back, after I edited it of course, I noticed that I mentioned continuity is not possible at Endpoints. This is NOT true, as we can consider one-sided limits. What I MEANT was that since we must consider an OPEN INTERVAL of continuity in the NEIGHBORHOOD of our point, the points we are checking must NOT be at endpoints of continuity. If they are, a neighborhood around those points is not possible. I failed to make a distinction between continuity and continuity in the NEIGHBORHOOD around a point. I am TERRIBLY sorry about the deception. So, one more time; continuity IS possible at an endpoint, but the points we are checking must show continuity on an OPEN interval of continuity to satisfy the NEIGHBORHOOD around the point. Therefore, if a point we are checking falls on the endpoint of continuity, this fails our theorem. When I refer to Continuity around the point, I mean exactly that... the neighborhood around that point, not just continuity of the function, but continuity on a open interval around the initial value. I know that I make reference to that EXACT statement several times in the video, but it was not clear enough in the beginning of the video. I assumed that the distinction would be understood and that my usage of Continuity would be limited to the Continuity of the function in the neighborhood of the point we are CHECKING, and that was my mistake. I tried to make it understandable and made a fundamental error. When I refer to "the function is not continuous at an endpoint", my meaning is that if the INITIAL VALUE is at the endpoint of an interval of continuity, we fail to have continuity on an OPEN INTERVAL.... a NEIGHBORHOOD around that point. Continuity HERE is an "open" idea because of the necessity of continuity in the NEIGHBORHOOD around our point.. My apologies for any misunderstandings this may have caused. In my mind, as I was filming this, it was clear but just keep in mind that when we refer to continuity here, it's continuity on an OPEN interval around the POINT WE ARE CHECKING. Hope this helps.
How to determine existence of solutions to Differential Equations and when those solutions will be Unique.
Комментарии
 0:12:22
0:12:22
 0:03:52
0:03:52
 0:44:32
0:44:32
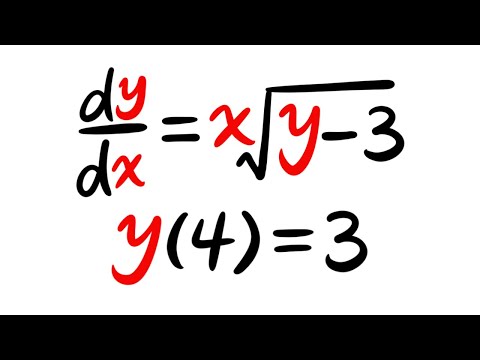 0:11:22
0:11:22
 0:07:23
0:07:23
 0:13:15
0:13:15
 0:06:53
0:06:53
 0:10:03
0:10:03
 1:16:28
1:16:28
 0:06:23
0:06:23
 0:03:31
0:03:31
 0:07:31
0:07:31
 0:34:37
0:34:37
 0:06:41
0:06:41
 0:07:25
0:07:25
 0:07:30
0:07:30
 0:11:19
0:11:19
 0:15:40
0:15:40
 0:06:03
0:06:03
 0:07:55
0:07:55
 0:08:16
0:08:16
 0:06:29
0:06:29
 0:17:11
0:17:11
 0:05:37
0:05:37