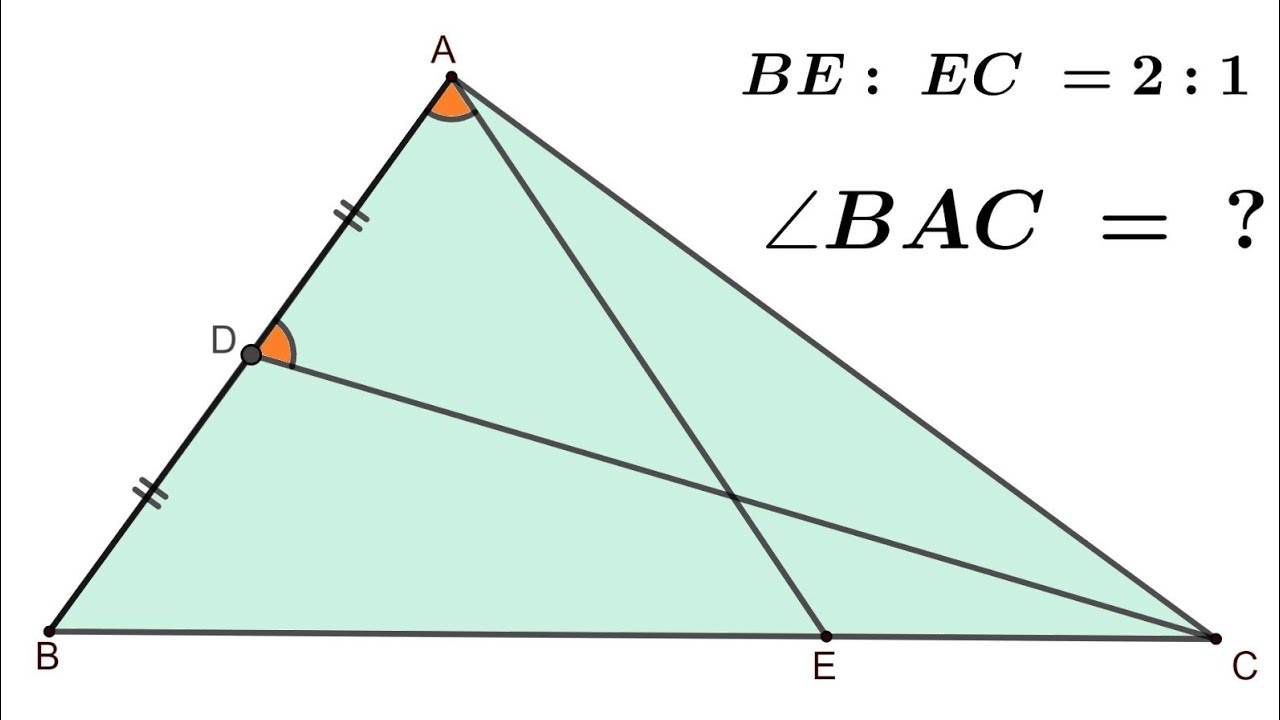
Find ∠ BAC. || Angle Chasing.|| ∠BAE = ∠ADC.|| BE : EC = 2 : 1. || Triangles with common vertex.

In this video clip, we have to find the value of ∠ BAC. It is an angle chasing problem.

In a ∆ ABC, D is the mid point of AB. E is a point on BC such that BE : EC = 2 : 1. Given that ∠BAE = ∠ADC.

#Geometry
#Right_Triangle
#Triangles_with_common_vertex.
#Angle_Chasing_Problem

Useful for :
#NTSE, #GRE, #IITJEE, #IOQM, #RMO, #INMO, #ISI, #CMI, #MAT, #CAT, #SAT, #BITSAT, #PET, #CET, #MCA, #NDA, #CDS, #SSC, #KVPY, #RRB, etc...

[dannymeslier]

Cheers!
My solution:
From point D, draw a line parallel to BC. It intersects EA in H. DH is half of BE and is therefore equal to EC. By angle-angle-side, GHD and GEC are congruent, so DG is equal to GC and they're both equal to AG.

[spiderjump]

Let F be the point of intersection of AE and CD .
Let area of triangle FEC be e and the area of FAC be d.
Area of BFE =2e (BE=2EC)
Area of BAF=2x area of AEC( BE=2EC)
= 2(e+d)
So area of ABF= 2d
Area of ADF=area of BDF(AD=BD)
Hence area of ADF=d=area ofAFC
Since the 2 triangles have same vertex and height, DF=FC
FA=DF ( isosceles triangle)
=FC
So triangles AFC and triangles AFD are isosceles, so let angle DAF=x and angle FAC=y
In triangle ADC, 2x+2y=180
x+y=angle BAC=90