filmov
tv
CompX: Mathematics of PCA - Covariance matrices
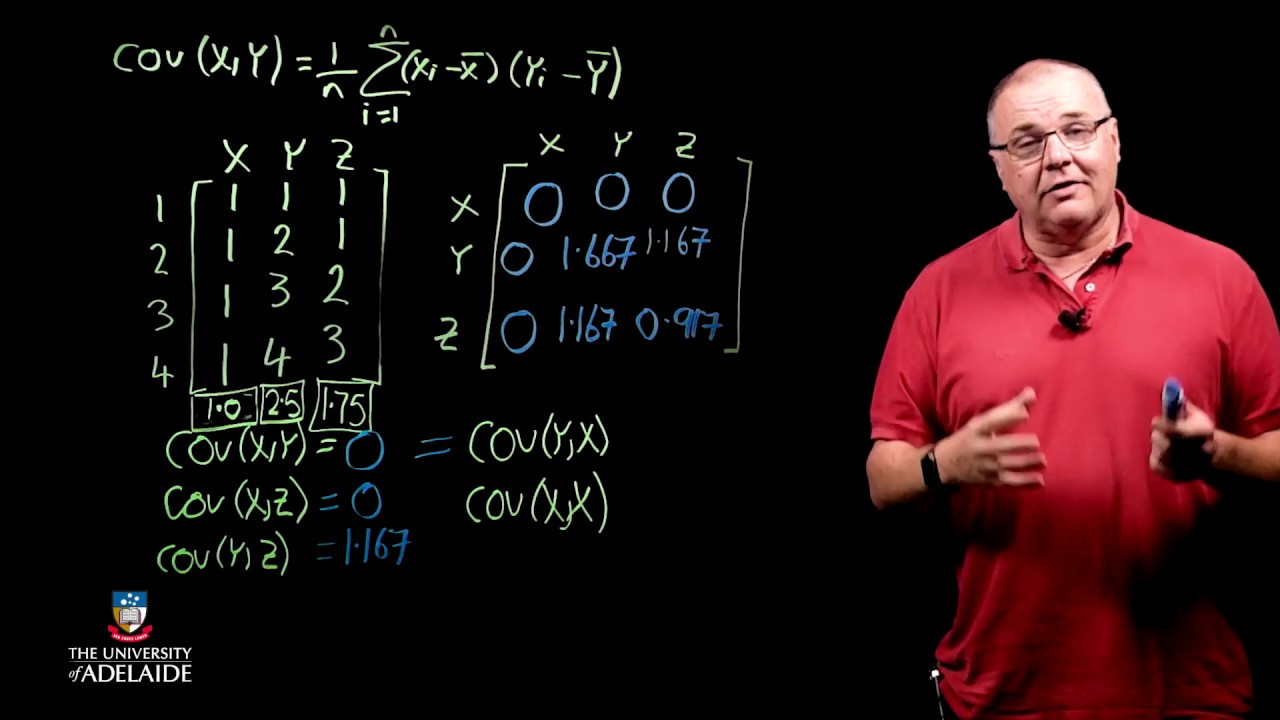
Показать описание
Computational Thinking and Big Data is part of the Big Data MicroMasters program offered by The University of Adelaide and edX.
Learn the core concepts of computational thinking and how to collect, clean and consolidate large-scale datasets.
Enrol now!
Learn the core concepts of computational thinking and how to collect, clean and consolidate large-scale datasets.
Enrol now!
CompX: Mathematics of PCA - Matrices
CompX: Mathematics of PCA - Covariance matrices
Mathematics of PCA
StatQuest: Principal Component Analysis (PCA), Step-by-Step
Principal Component Analysis (PCA) Explained: Simplify Complex Data for Machine Learning
Principal Component Analysis (The Math) : Data Science Concepts
Lecture: Principal Componenet Analysis (PCA)
Principal Component Analysis (PCA)
PCA Mathematics behind it (Part01)
PCA explained with math
Mathematics of PCA
Principal Component Analysis (PCA) : Intuitive Perspective
Principal Component Analysis (PCA) - THE MATH YOU SHOULD KNOW!
Principal Component Analysis (PCA) Explained in simplest way
the Meaning of Covariance Matrix and PCA
Principal Components Analysis (PCA) Tutorial Part 1/3: Basis
Shape Analysis (Lectures 18, extra content): Manifold optimization for PCA problems
Principal Component Analysis (PCA)
Harvard AM205 video 2.13 - An example of PCA
Visualisation of high-dimensional data: a brief mathematical introduction to PCA and t-SNE
PCA: example - Steps 1 & 2
Principal Component Analysis (PCA) for Reduction and Whitening - Linear Algebra Tutorial
1) PCA overview
Coding PCA from Scratch : Data Science Code
Комментарии
 0:03:14
0:03:14
 0:05:07
0:05:07
 0:03:11
0:03:11
 0:21:58
0:21:58
 0:08:49
0:08:49
 0:13:59
0:13:59
 0:51:13
0:51:13
 0:13:46
0:13:46
 0:23:16
0:23:16
 0:22:23
0:22:23
 0:15:10
0:15:10
 0:16:46
0:16:46
 0:10:06
0:10:06
 0:09:02
0:09:02
 0:23:29
0:23:29
 0:03:40
0:03:40
 0:30:18
0:30:18
 0:26:34
0:26:34
 0:25:49
0:25:49
 0:15:48
0:15:48
 0:10:30
0:10:30
 0:05:08
0:05:08
 0:05:35
0:05:35
 0:05:30
0:05:30