filmov
tv
How Do You Find The Shape of Hanging Rope? Classic Physics Problem

Показать описание
When you hang up a rope between two points under the weight of gravity, it makes a distinctive arc-like shape that anyone can instinctively recognize. In this video, I'll show you how to actually derive the shape---and find the mathematical function that describes it---using F = ma and a little calculus.
About the classic physics problem series:
In these intro-to-intermediate-level physics videos, I'll discuss classic physics "challenge" problems that you might meet in your introductory mechanics and electromagnetism classes. They might be based on simple concepts, but these problems can still get pretty tough!
About me:
How to EASILY Find and defeat Billy Fortnite
Fortnite NEW Billy Boom and Chainsaw location and Gameplay - Where to Find Billy Boom and Chainsaw
Can you find all the hidden animals? - QUIZ
*NEW* How To Do Jigsaw's Challenge In Fortnite❗(Everything You NEED To Know About It)
7 Days Exploring An Underground City
FIND the MARKERS *How To Get ALL 25 NEW Markers and Badges* CANDYLAND UPDATE! Roblox
Fortnitemares 2024 Gameplay Trailer
How to Find the Mode | Math with Mr. J
How do you find the degree of a polynomial
IF YOU SEE THIS BLOODY LITTLE GIRL AT YOUR DOORSTEP, DO NOT LET HER IN! (SHE'S CURSED)
How to Find the Mean | Math with Mr. J
How to Count Music | Exercise to help you find the beat in a song
How to Find the Median | Math with Mr. J
IF YOU SEE BLOOD ON A FIRETRUCK, GET HELP FAST! (you're in DANGER)
FIND THE MARKERS *How To Get ALL 151 Markers and Badges* Roblox
(DAY 8) How To Find ALL 30 PURPLE PUMPKIN LOCATIONS In Adopt Me Halloween Event 2024! Roblox
How do you find the center of a circle? (Geometry)
How To Find End Portal In Minecraft - Full Guide
How To Find Your Passion
New BIND Glove⛓️ & HOW TO GET IT! - Slap Battles Roblox (ft. Gravity!)
How Do You Find The Shape of Hanging Rope? Classic Physics Problem
How to find lost stuff ¦ Five top tips
how to find the degree of an angle using a speed square
How To Find the Beat and Dance on Rhythm (Follow Along!)
Комментарии
 0:01:44
0:01:44
 0:03:42
0:03:42
 0:06:08
0:06:08
 0:12:27
0:12:27
 0:20:35
0:20:35
 0:25:42
0:25:42
 0:01:03
0:01:03
 0:04:07
0:04:07
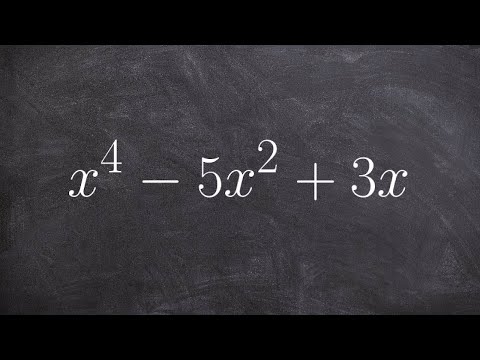 0:02:48
0:02:48
 0:20:46
0:20:46
 0:03:33
0:03:33
 0:00:43
0:00:43
 0:05:33
0:05:33
 0:21:18
0:21:18
 1:39:57
1:39:57
 0:09:45
0:09:45
 0:04:14
0:04:14
 0:04:34
0:04:34
 0:05:42
0:05:42
 0:08:44
0:08:44
 0:13:38
0:13:38
 0:04:36
0:04:36
 0:01:13
0:01:13
 0:05:27
0:05:27