filmov
tv
Solving Homogeneous First Order Differential Equations (Differential Equations 21)

Показать описание
Exercises in Solving Homogeneous First Order Differential Equations with Separation of Variables. A review of various integration techniques is included.
Homogeneous Differential Equations
Solving Homogeneous First Order Differential Equations (Differential Equations 21)
How To Solve First Order Homogeneous Differential Equation
Oxford Calculus: Solving Homogeneous First Order Differential Equations
Substitutions for Homogeneous First Order Differential Equations (Differential Equations 20)
Homogeneous Differential Equations (introduction & example)
🔵11 - Homogeneous First Order Differential Equations (Solved Examples)
Determine if a First-Order Differential Equation is Homogeneous - Part 1
bsc 2nd year partial differential equation chapter 4 | partial differential equation ba 2nd year
Differential Equation - 1st Order, Linear Form (2 of 9) Example of Homogenous Equation
Systems of linear first-order odes | Lecture 39 | Differential Equations for Engineers
Diff Eqn: Solving first order homogeneous equation 1/6
🔵10 - Homogeneous Functions (Intro to Homogeneous First Order Differential Equations)
4 Types of ODE's: How to Identify and Solve Them
Homogeneous First-Order Differential Equations (Introduction)
Homogeneous First Order Differential Equations
Homogeneous first order ordinary differential equation
How to Solve Constant Coefficient Homogeneous Differential Equations
How to Solve First Order Linear Differential Equations
First Order Linear Differential Equations
First Order Homogeneous Differential Equations Lesson 2
First order, Ordinary Differential Equations.
Separable First Order Differential Equations - Basic Introduction
Solve a First-Order Homogeneous Differential Equation - Part 2
Комментарии
 0:26:55
0:26:55
 1:55:11
1:55:11
 0:08:33
0:08:33
 0:24:42
0:24:42
 1:05:45
1:05:45
 0:07:59
0:07:59
 0:42:58
0:42:58
 0:07:47
0:07:47
 0:57:22
0:57:22
 0:03:49
0:03:49
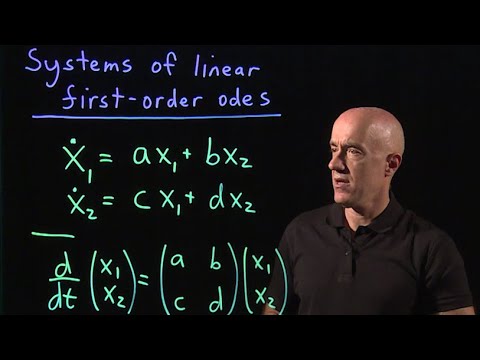 0:08:28
0:08:28
 0:07:29
0:07:29
 0:16:18
0:16:18
 0:06:57
0:06:57
 0:08:00
0:08:00
 0:14:16
0:14:16
 0:07:32
0:07:32
 0:06:41
0:06:41
 0:10:53
0:10:53
 0:22:28
0:22:28
 0:06:16
0:06:16
 0:48:35
0:48:35
 0:10:42
0:10:42
 0:10:31
0:10:31