filmov
tv
Brown Numbers - Numberphile
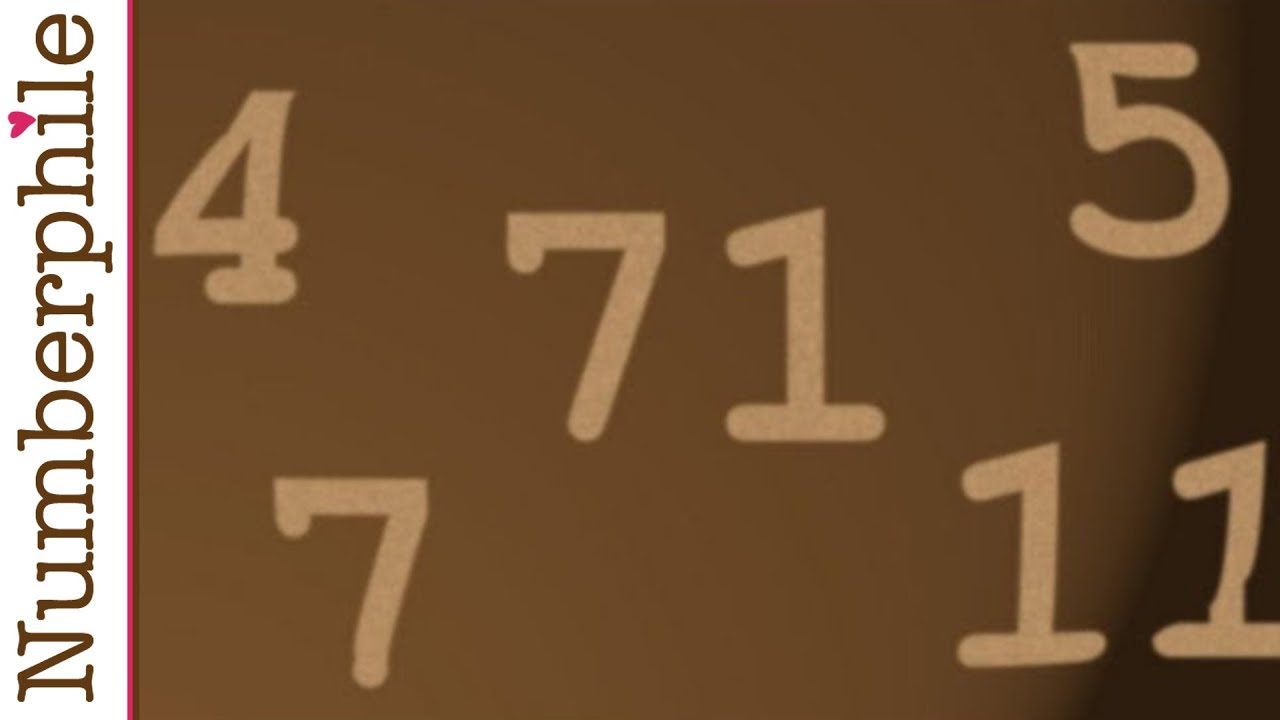
Показать описание
More links & stuff in full description below ↓↓↓
There are only three pairs of Brown Numbers - and only five of the numbers themselves (because 5 is repeated)... At least we think that's all of them? No-one has proven it. This is called Brocard's Problem and has been entertained by great mathematicians such as Paul Erdos.
The Brown Numbers are (5,4) (11,5) and (71,7).
NUMBERPHILE
Videos by Brady Haran
There are only three pairs of Brown Numbers - and only five of the numbers themselves (because 5 is repeated)... At least we think that's all of them? No-one has proven it. This is called Brocard's Problem and has been entertained by great mathematicians such as Paul Erdos.
The Brown Numbers are (5,4) (11,5) and (71,7).
NUMBERPHILE
Videos by Brady Haran
Brown Numbers - Numberphile
Brown's Criterion - Numberphile
Illegal Numbers - Numberphile
WARNING: Contains Numbers
The Golden Ratio (why it is so irrational) - Numberphile
The Daddy of Big Numbers (Rayo's Number) - Numberphile
Favourite Numbers - Numberphile
Prime Pyramid (with 3Blue1Brown) - Numberphile
Chinese Lucky Numbers - Numberphile
The Prime Number Race (with 3Blue1Brown) - Numberphile
Bertrand's Paradox (with 3blue1brown) - Numberphile
The Forgotten Number System - Numberphile
A Number Sequence with Everything - Numberphile
The Reciprocals of Primes - Numberphile
7 and Happy Numbers - Numberphile
Paterson Primes (with 3Blue1Brown) - Numberphile
2.920050977316 - Numberphile
Spaghetti Numbers - Numberphile
But what is the Central Limit Theorem?
The Legend of Question Six - Numberphile
37 - Numberphile
That Viral Math Problem (Cheryl's Birthday) - Numberphile
Euler's Formula - Numberphile
A Problem with Rectangles - Numberphile
Комментарии
 0:04:05
0:04:05
 0:07:56
0:07:56
 0:05:59
0:05:59
 0:05:34
0:05:34
 0:15:13
0:15:13
 0:15:26
0:15:26
 0:07:43
0:07:43
 0:10:53
0:10:53
 0:08:08
0:08:08
 0:20:29
0:20:29
 0:10:43
0:10:43
 0:10:21
0:10:21
 0:10:55
0:10:55
 0:15:31
0:15:31
 0:01:33
0:01:33
 0:10:35
0:10:35
 0:12:42
0:12:42
 0:03:28
0:03:28
 0:31:15
0:31:15
 0:08:45
0:08:45
 0:02:58
0:02:58
 0:11:34
0:11:34
 0:21:23
0:21:23
 0:17:12
0:17:12