filmov
tv
The Reciprocals of Primes - Numberphile

Показать описание
Matt Parker explores the work of William Shanks - and boots up the ShanksBot.
More links & stuff in full description below ↓↓↓
NUMBERPHILE
Videos by James Hennessy and Brady Haran
More links & stuff in full description below ↓↓↓
NUMBERPHILE
Videos by James Hennessy and Brady Haran
The Reciprocals of Primes - Numberphile
The Reciprocal Prime Series (this proof should be taught in calculus!)
a nice property about reciprocals of primes.
The sum of the reciprocals of all primes diverges | #some2
The Sum of All Prime Twins
reciprocals of twin primes
The Prime Number Race (with 3Blue1Brown) - Numberphile
The series of reciprocals of prime numbers
What's a Reciprocal? | Math with Mr. J
Fool-Proof Test for Primes - Numberphile
Prime Reciprocal Series with @blackpenredpen (Oxford Maths Interview Question)
A harmonic series with only primes.
11 4 Erdos s proof on divergence of reciprocals of primes
Twin Primes & Bruns Theorem
The High Schooler Who Solved a Prime Number Theorem
EASIEST proof that the sum of the reciprocals of the primes diverges!
Sum of the reciprocals of primes
11.4 Erdos_s proof on divergence of reciprocals of primes
Paterson Primes (with 3Blue1Brown) - Numberphile
EASIEST proof that the sum of the reciprocals of the primes diverges!
The Most Wanted Prime Number - Numberphile
The Prime Problem with a One Sentence Proof - Numberphile
sum of the reciprocals of the primes is divergent
Peculiar Primes Ep. 1: Prime Reciprocals and Mysterious Repeating Decimals
Комментарии
 0:15:31
0:15:31
 0:11:44
0:11:44
 0:07:42
0:07:42
 0:07:34
0:07:34
 0:05:05
0:05:05
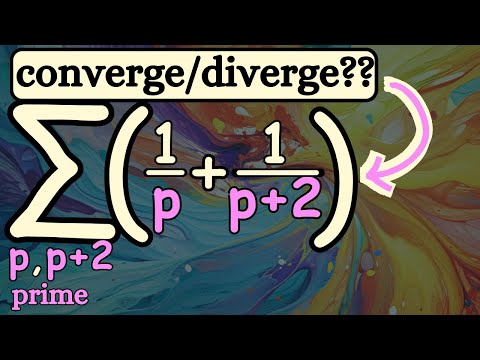 0:15:11
0:15:11
 0:20:29
0:20:29
 0:10:32
0:10:32
 0:03:20
0:03:20
 0:03:43
0:03:43
 0:22:09
0:22:09
 0:14:13
0:14:13
 0:18:03
0:18:03
 0:02:32
0:02:32
 0:05:15
0:05:15
 0:09:37
0:09:37
 0:17:54
0:17:54
 0:18:03
0:18:03
 0:10:35
0:10:35
 0:10:07
0:10:07
 0:08:35
0:08:35
 0:06:42
0:06:42
 0:06:05
0:06:05
 0:11:15
0:11:15