filmov
tv
A Problem with Rectangles - Numberphile

Показать описание
More links & stuff in full description below ↓↓↓
NUMBERPHILE
Videos by Brady Haran
NUMBERPHILE
Videos by Brady Haran
A Problem with Rectangles - Numberphile
Rectangle Problem (extra) - Numberphile
Find if two rectangles overlap | GeeksforGeeks
rectangles | rectangle area | geometry problems | Masterclass Geometry
Example Problems with Rectangles
Math for fun, how many rectangles?
12 - Generic Rectangles (How They Work)
Who cares about topology? (Inscribed rectangle problem)
KHR25 - IX CBSE MATHS BG 21/08/2024 - Heron's Formula
What Is The Rectangle's Area?
An evil geometry question - the 6 rectangles problem
Problem A : Packing Rectangles | Codeforces EDU Section | Binary Search | Step 2 | Explan. and Code
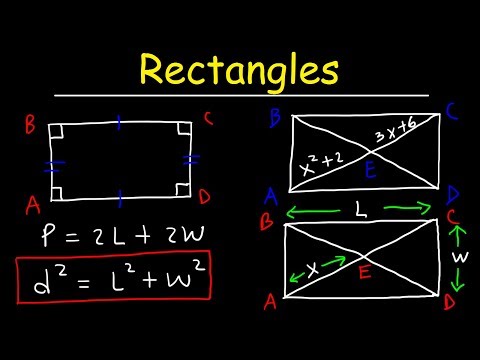
Rectangles - Properties of Parallelograms, Special Quadrilaterals - Geometry
Word problem involving the area between rectangles
Use a chart to understand how rectangles can have the same perimeter with different areas
Problem Solving with Area and Perimeter of Rectangles (Version 1)
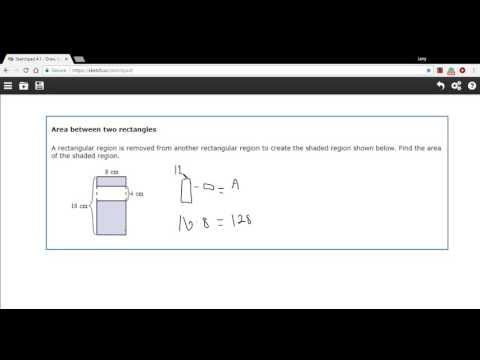
Area between two rectangles
How many rectangles are there? Can you count?
Geometry Word Problem 'Rectangles'
Word problems with Rectangles #onlineMaths #mathtutorials #shorts @EndzeMathsSolutions
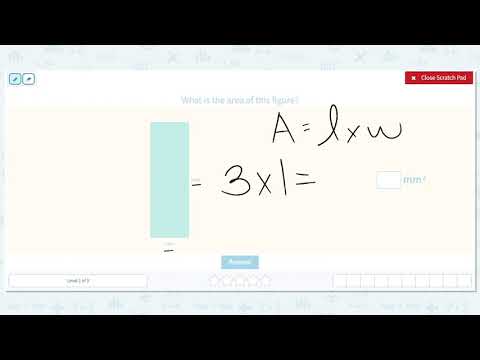
Area of rectangles - varied problems
A tricky problem in rectangles | Olympiads, Bank PO, IBPS, PRMO NMTC IMO
Area Problems with Triangles and Rectangles
3.15 Area of Rectangles
Комментарии
 0:17:12
0:17:12
 0:05:14
0:05:14
 0:05:18
0:05:18
 0:02:50
0:02:50
 0:04:08
0:04:08
 0:13:54
0:13:54
 0:01:37
0:01:37
 0:18:16
0:18:16
 1:00:14
1:00:14
 0:02:48
0:02:48
 0:04:35
0:04:35
 0:13:31
0:13:31
 0:12:26
0:12:26
 0:03:23
0:03:23
 0:04:08
0:04:08
 0:04:39
0:04:39
 0:01:23
0:01:23
 0:01:20
0:01:20
 0:02:09
0:02:09
 0:00:42
0:00:42
 0:09:29
0:09:29
 0:05:54
0:05:54
 0:06:29
0:06:29
 0:05:29
0:05:29