filmov
tv
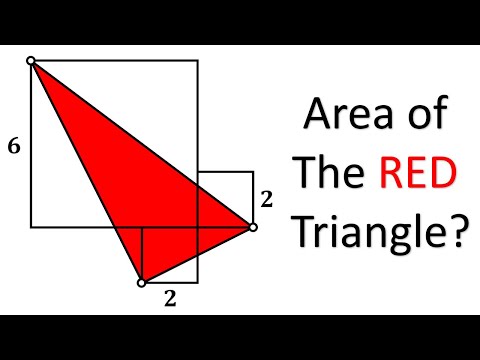
Area of Red Triangle
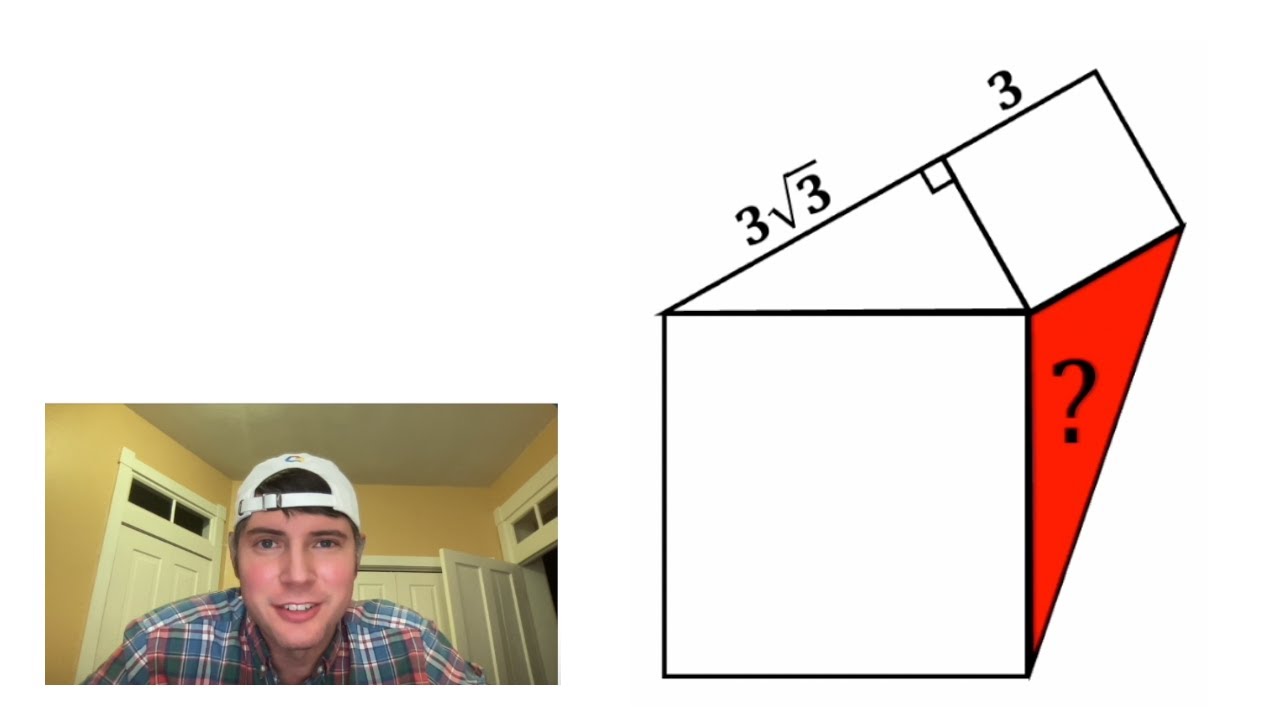
Показать описание
Area of Red Triangle
Area of Red Triangle
What’s the area of the red triangle?
The EASIEST and FASTEST way to find the area of a Triangle
Find Area of Red Triangle #geometry #circles
Can you find the area of the Red shaded triangle? | (Four triangles in a squares) | #math #maths
Find the Area of Red Triangle. Easy and Geometry Problem.
Area of a Triangle | MathHelp.com
Math Level 1 || Area of right angle triangle, rectangle and square
Geometry | Finding the Area of the Red Shaded Right Triangle
Area of Red Triangle Challenge
In-depth explanation | Can you find area of the Red shaded triangle? | #math #maths #mathematics
📐 type of triangle 📐
Survivor Says Something New About the Bermuda Triangle Mystery
The Bermuda Triangle Mystery Has Been Solved
Find Area of Red Triangle | Geometry Skills
How to Find the Area of a Triangle | Calculate the Area of a Triangle
Area of red triangle is side rectangle - Legend of math - 1.13.5.2020
Find The Area Of The Red Triangle|| #shorts #ytshorts #mathgame #mathstricks #bobby
What do red triangles at pro-Palestinian protests symbolize?
Can you find area of the Red shaded triangle in the Trapezoid? | (Trapezium) | #math #maths
Finding the Area of a Triangle | A Step-By-Step Guide | Math with Mr. J
Can you find the area of the triangle ABC? | (Step-by-step explanation) | #math #maths
Math Puzzle | The Area of the Given Shaded Triangle?
Комментарии
 0:03:35
0:03:35
 0:02:07
0:02:07
 0:00:06
0:00:06
 0:05:20
0:05:20
 0:00:59
0:00:59
 0:09:55
0:09:55
 0:03:34
0:03:34
 0:01:36
0:01:36
 0:58:08
0:58:08
 0:11:02
0:11:02
 0:04:32
0:04:32
 0:08:09
0:08:09
 0:00:05
0:00:05
 0:09:08
0:09:08
 0:04:30
0:04:30
 0:09:26
0:09:26
 0:06:37
0:06:37
 0:03:54
0:03:54
 0:00:06
0:00:06
 0:03:22
0:03:22
 0:09:03
0:09:03
 0:07:35
0:07:35
 0:08:19
0:08:19
 0:18:20
0:18:20