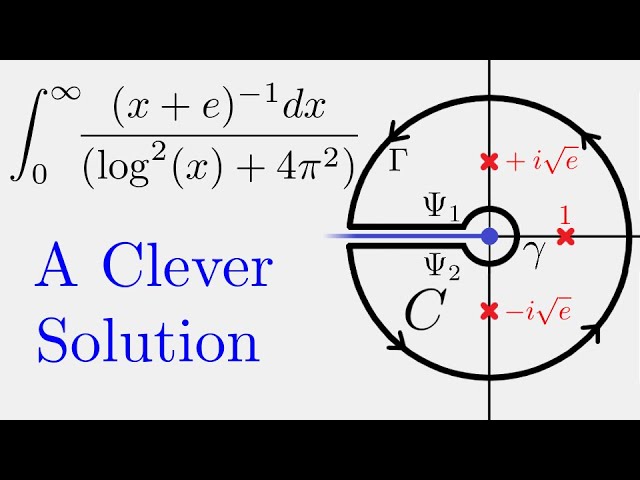
Complex Analysis: Nasty Integral with Elegant Solution

Показать описание

Today, we evaluate a very difficult-looking integral (at least for real methods) using complex analysis.

qncubed3

Рекомендации по теме

Комментарии

Nice video- for a real analytic method, you can use the representation: 1/(pi^2+(ln x)^2)=1/pi * int_0^\infty cos(ln (x)t) * e^(-pi * t) dt and then write cos(z) as the Re(e^(i z))

KStarGamer_

That was literally one of the best integral videos i've ever seen.

비선형편미분방정식

nice, solving integrals is so much fun

silentintegrals

That's enough: 🤓
I can't wait for your next video.
Thank you *QN³* 💗

wuyqrbt

You can also decompose directly
I = 1/(4Pi*i) * Int_0^\infty dx/(x+e) * ( 1/(log(x)-2Pi*i) - 1/(log(x)+2Pi*i) )
= 1/(4Pi*i) * PV Int_0^\infty dx/(x+e) * ( 1/log(x) - 1/(log(x)+2Pi*i) ) + 1/(-4Pi*i) * PV Int_0^\infty dx/(x+e) * ( 1/log(x) - 1/(log(x)-2Pi*i) )
= f + f*
where f* is the complex conjugate of f and PV stands for principal value.
f is then evaluated by considering
F=1/(4Pi*i)*Int_{C1+C2+Gamma) dz/(z+e) * 1/log(z) = 2Pi*i/(4Pi*i)*1/log(-e) = 1/2 * 1/(1+i*Pi))
where the branch cut is put a along (0, \infty). The contour is counter-clockwise and C1=(R-i0, -i0), C2=(i0, R+i0), Gamma=(|z|=R).
The integral along Gamma is zero since R/(R-e) * 1/log(R) tends to zero as R->infinity. Furthermore, on C1: arg(z)=2Pi and on C2: arg(z)=0.
Int_{C1} dz/(z+e) * 1/log(z) = Int_{R-i0}^{-i0} dz/(z+e) * 1/log(z) = - Int_{0}^{R} dz/(z+e) * 1/(log(z)+2Pi*i). Adding a PV here doesn't change the result.
Int_{C2} dz/(z+e) * 1/log(z) = PV Int_{0}^{R} dz/(z+e) * 1/log(z) - i*Pi*Res( 1/(z+e) * 1/log(z) )|_{z=1} = PV Int_{0}^{R} dz/(z+e) * 1/log(z) - i*Pi/(1+e). Then,
F=f - i*Pi/(4Pi*i) * 1/(1+e) = f - 1/4*1/(e+1). Finally,
1/(1+Pi^2)=F+F*= f+f* - 1/2*1/(e+1).

digxx

How do you you do residue at infinity for essential singularities?

juniorcyans

Is it possible to use something similar to solve this? -e^{(aj^2 + b)M}}{1-e^{aj^2 +b}}

LucaHerrtti

Complex Analysis: Nasty Integral with Elegant Solution

Complex Analysis: Nasty Integral with Elegant Solution

Complex Analysis: Another Integral Snack

Cauchy Integral Formula with Examples - Complex Analysis by a Physicist

A stellar integral solved using some wonderful complex analysis

Complex Analysis: Integral of log(x)/(x+1)^2

Complex Analysis L08: Integrals in the Complex Plane

Evaluating Real Integrals With Cauchy's Residue Theorem - Complex Analysis By A Physicist

Complex Analysis: Integral of 1/(x^n+1) feat. pizza contour

Complex Analysis: Integral of 1/(x^4-x^2+1) using Contour Integration

Complex Analysis 26 | Keyhole contour

EX: A contour integral with higher-order poles

Complex Analysis: An Integral from @MichaelPennMath

Complex Analysis L10: Cauchy Integral Formula

Complex Analysis: Cauchy's Integral Theorem

Complex Analysis L09: Complex Residues

Complex Analysis: Integral of sech(ax) using Contour Integration

Complex Analysis: Integral of log(x^2+1)/x^2

Complex Analysis - Line Integrals

Complex Analysis: Double Keyhole Contour

Complex Analysis: One EXOTIC Integral

Complex Analysis-ing a CRAZY Integral

Complex Analysis: Is this solution way too overkill?

Outtakes - Integral of ln(x)/(x^n+1) with Complex Analysis

Insane Contour Integral from @maths_505 !