filmov
tv
Complex Analysis: Integral of 1/(x^n+1) feat. pizza contour

Показать описание
Today, we revisit an old classic on the channel, the integral from 0 to infinity of 1/(x^n+1) where n is any real number greater than 1.
Complex Analysis: Integral of 1/(x^n+1) feat. pizza contour
Integral of 1/(x^n+1) from 0 to infinity
Integral 1/x^n + 1 from 0 to infinity
Complex Analysis: Integral of ln(x)/(x^n+1) using Contour Integration
The integral 1/(x+1) and x^(n-1)/(x^n+b)
Integral 1/x^n + 1 from 0 to infinity
Complex Analysis: Integral of (x^n)/(x+1) using Contour Integration
One Sick Integral!
Integral of x^(n - 1)/(x^n + a)^n
Integral of 1/(x^2+1) from -inf to inf, Contour Integral
Integration x^n-1 e^-h²x² from 0 to infinity | Gamma Functions
new CONTRIBUTION 2 Complex Analysis Integral of 1 x^n+1
IIT Bombay CSE 😍 #shorts #iit #iitbombay
CONTRIBUTION 2 Complex Analysis Integral of 1 x^n+1 fea
If `I(m,n)=int_0^1x^(m-1)(1-x)^(n-1)dx`, then
The Integral of 1/x EXPLAINED. It's NOT what you think...
Complex Analysis | Unit 2 | Lecture 13 | Example of Cauchy's Integral Formula
1st yr. Vs Final yr. MBBS student 🔥🤯#shorts #neet
Complex Analysis: Integral of 1/(x^4+1) using Contour Integration
Suites des intégrales de f_n(x)=x^n/(1+x) sur [0;1]
Salsa Night in IIT Bombay #shorts #salsa #dance #iit #iitbombay #motivation #trending #viral #jee
When mathematicians get bored (ep1)
Interesting Integral-1: ∫(𝒙^𝒎 (𝐥𝐨𝐠𝒙 )^𝒏) 𝒅𝒙=(−𝟏)^𝒏 𝒏!/((𝒎+𝟏)^((𝒏+𝟏))...
Before JEE vs After JEE 😍 | My Transformation💔 | IIT Motivation|Jee 2023 #transformation #iit #viral...
Комментарии
 0:36:33
0:36:33
 0:07:29
0:07:29
 0:23:31
0:23:31
 0:29:50
0:29:50
 0:03:49
0:03:49
 0:10:39
0:10:39
 0:50:28
0:50:28
 0:19:45
0:19:45
 0:02:50
0:02:50
 0:19:50
0:19:50
 0:08:00
0:08:00
 0:01:07
0:01:07
 0:00:11
0:00:11
 0:04:57
0:04:57
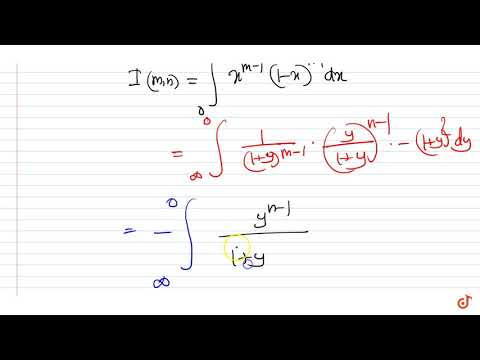 0:04:20
0:04:20
 0:03:12
0:03:12
 0:09:05
0:09:05
 0:00:20
0:00:20
 0:16:15
0:16:15
 0:05:20
0:05:20
 0:00:14
0:00:14
 0:00:37
0:00:37
 0:07:46
0:07:46
 0:00:20
0:00:20