filmov
tv
Evaluating Real Integrals With Cauchy's Residue Theorem - Complex Analysis By A Physicist

Показать описание
In this video we go over what is one of the most important and useful applications of Cauchy's Residue Theorem, evaluating real integrals with Residue Theorem. This may seem a bit confusing. How can we evaluate a real integral with a complex analysis theorem? The answer is very interesting and opens up the ability to evaluate many different kinds of integrals via analytic means.
Music: Mirror Mind By Bobby Richards
Music: Mirror Mind By Bobby Richards
Evaluating Real Integrals With Cauchy's Residue Theorem - Complex Analysis By A Physicist
Complex Analysis | Unit 2 | Lecture 13 | Example of Cauchy's Integral Formula
evaluating real trig integrals with cauchy s res 2
Complex Analysis 35 | Application of the Residue Theorem
Basic Complex Analysis - Unit 3 - Lecture 18 - Evaluation of Integral using Cauchy's Residue Th...
How REAL Men Integrate Functions
Complex integration, Cauchy and residue theorems | Essence of Complex Analysis #6
Complex Analysis L10: Cauchy Integral Formula
Complex integration Cauchy Integral formula Solved problem Belief physics
Lecture 14: Evaluating real integrals via Cauchy residue formula
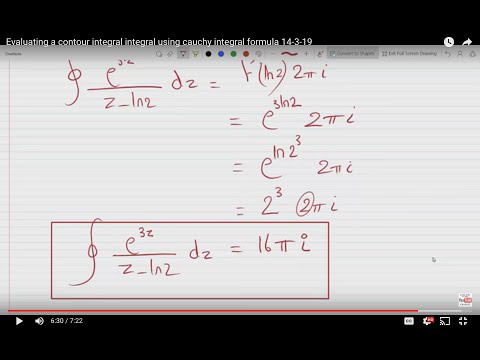
Evaluating a Contour Integral using Cauchy Integral Formula 14-3-19
Computing Improper Integrals using the Residue Theorem | Cauchy Principal Value
This chapter closes now, for the next one to begin. 🥂✨.#iitbombay #convocation
🔥 POV: Integration - Look at me! 👀 💪 | JEE 2024 | Math | Bhoomika Ma'am
Complex Analysis- Contour Integration | Application of Residue Theorem
Tamasha Dekho 😂 IITian Rocks Relatives Shock 😂😂😂 #JEEShorts #JEE #Shorts
16. Cauchy's Theorem and Cauchy's Integral Formula | Problem#1 | Complete Concept
Cauchy's Integral Formula (Proof)
Contour Integration #5 - Cauchy's Integral Formula - LearnMathsFree
Cauchy's Residue Theorem Examples (Complex Analysis)
Basic Complex Analysis - Unit 3 - Lecture 17 - Residue Calculation at Simple Pole
Evaluation of contour integration using Cauchy's integral theorem and Cauchy's integral fo...
Evaluate the Line Integral over the Circle | z - i | = 2 CAUCHY'S INTEGRAL FORMULA
Jaldi Wahan Se Hato! IIT Delhi version! #iit #iitjee #iitdelhi
Комментарии
 0:16:06
0:16:06
 0:09:05
0:09:05
 0:17:36
0:17:36
 0:10:55
0:10:55
 0:06:14
0:06:14
 0:00:35
0:00:35
 0:40:45
0:40:45
 0:16:43
0:16:43
 0:08:27
0:08:27
 1:13:31
1:13:31
 0:07:09
0:07:09
 0:13:41
0:13:41
 0:00:16
0:00:16
 0:00:48
0:00:48
 0:23:08
0:23:08
 0:00:13
0:00:13
 0:08:09
0:08:09
 0:12:06
0:12:06
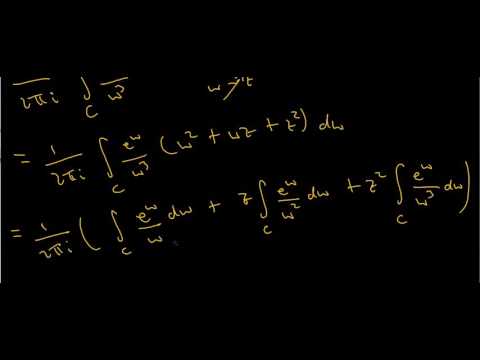 0:06:52
0:06:52
 0:35:50
0:35:50
 0:02:30
0:02:30
 0:28:32
0:28:32
 0:06:53
0:06:53
 0:00:17
0:00:17