filmov
tv
Proof: Composition of Injective Functions is Injective | Functions and Relations
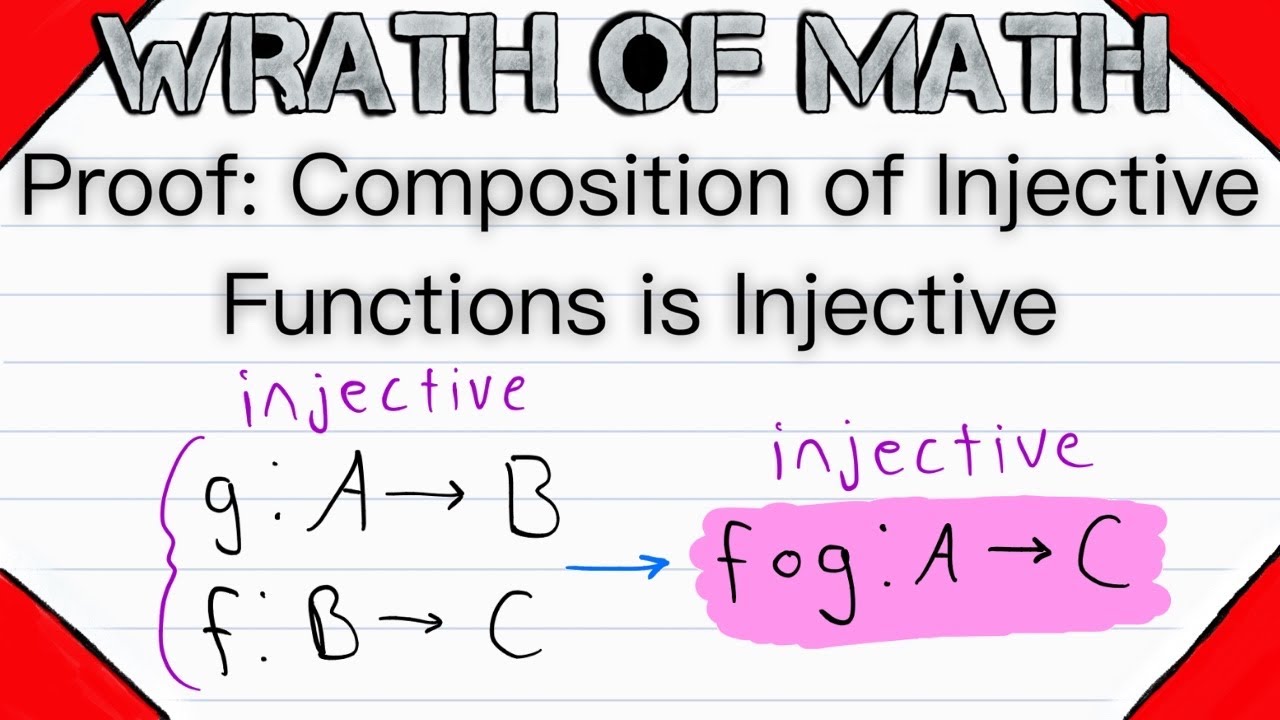
Показать описание
Let g and f be injective (one to one) functions, where g maps A to B and f maps B to C. Then the composition fog, which maps A to C, is also injective. We'll prove this result about injective functions and their compositions in today's lesson!
The proof is very straightforward, and merely requires us to apply the definition of injective functions a few times! Remember a function is injective if any two distinct elements in its domain are mapped to distinct elements in the codomain. In other words, injective functions preserve distinctness. And in this lesson we'll prove that function composition preserves injectiveness!
I hope you find this video helpful, and be sure to ask any questions down in the comments!
********************************************************************
The outro music is by a favorite musician of mine named Vallow, who, upon my request, kindly gave me permission to use his music in my outros. I usually put my own music in the outros, but I love Vallow's music, and wanted to share it with those of you watching. Please check out all of his wonderful work.
********************************************************************
+WRATH OF MATH+
Follow Wrath of Math on...
The proof is very straightforward, and merely requires us to apply the definition of injective functions a few times! Remember a function is injective if any two distinct elements in its domain are mapped to distinct elements in the codomain. In other words, injective functions preserve distinctness. And in this lesson we'll prove that function composition preserves injectiveness!
I hope you find this video helpful, and be sure to ask any questions down in the comments!
********************************************************************
The outro music is by a favorite musician of mine named Vallow, who, upon my request, kindly gave me permission to use his music in my outros. I usually put my own music in the outros, but I love Vallow's music, and wanted to share it with those of you watching. Please check out all of his wonderful work.
********************************************************************
+WRATH OF MATH+
Follow Wrath of Math on...
Комментарии
 0:07:25
0:07:25
 0:02:31
0:02:31
 0:04:17
0:04:17
 0:05:02
0:05:02
 0:02:26
0:02:26
 0:07:03
0:07:03
 0:03:35
0:03:35
 0:12:48
0:12:48
 0:13:33
0:13:33
 0:04:36
0:04:36
 0:08:18
0:08:18
 0:17:15
0:17:15
 0:07:15
0:07:15
 0:15:10
0:15:10
 0:04:43
0:04:43
 0:14:16
0:14:16
 0:00:19
0:00:19
 0:05:27
0:05:27
 0:04:01
0:04:01
 0:04:52
0:04:52
 0:04:12
0:04:12
 0:05:54
0:05:54
 0:02:57
0:02:57
 0:53:22
0:53:22