A Quick and Easy Radical Equation

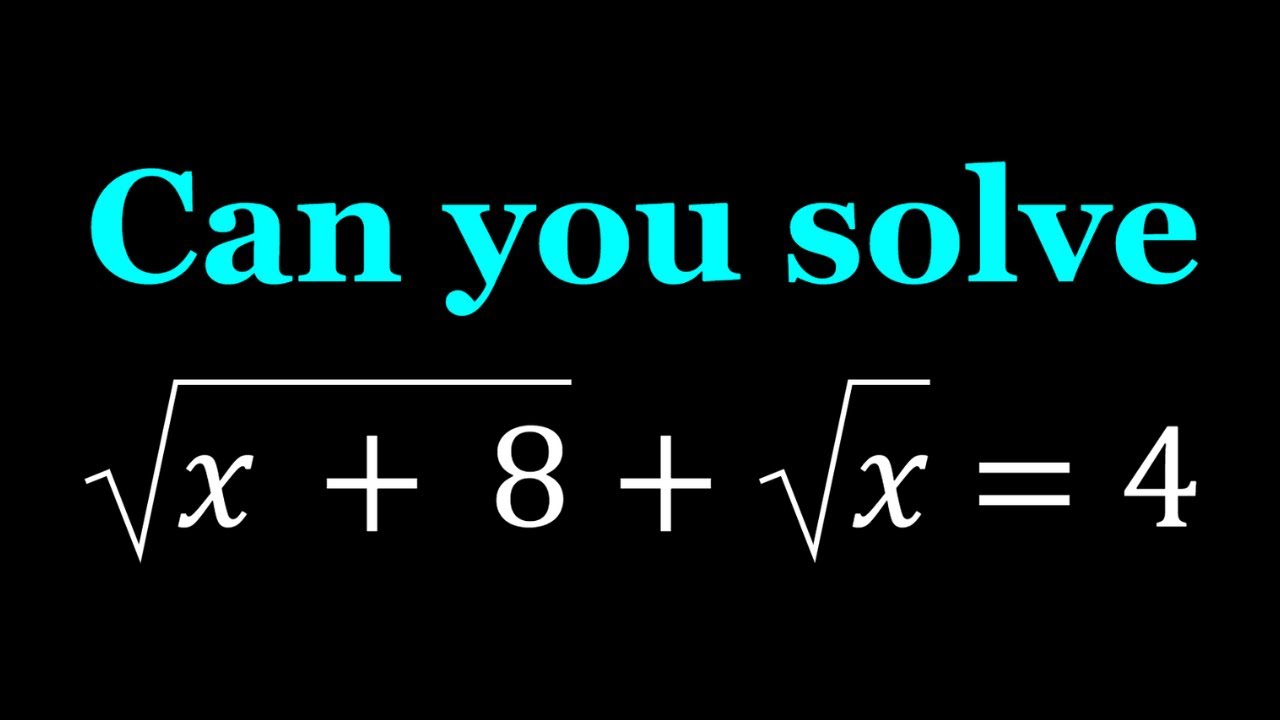
Показать описание

🤩 Hello everyone, I'm very excited to bring you a new channel (aplusbi)
Enjoy...and thank you for your support!!! 🧡🥰🎉🥳🧡

If you need to post a picture of your solution or idea:
sqrt(x+8)+sqrt(x)=4
#radicalequations #radicals #algebra
via @YouTube @Apple @Desmos @NotabilityApp @googledocs @canva

PLAYLISTS 🎵 :

SyberMath

Рекомендации по теме

Комментарии

You can shorten the second method a little bit by multiplying both sides of the original equation by √(x + 8) − √x straight away, which gives 8 = 4(√(x + 8) − √x), so √(x + 8) − √x = 2.

NadiehFan

For me, you re like the owner of Tom in Tom and Jerry cartoon

williamsomerset

3rd solution:
Square both sides:
=> 2x+8+2√x√(x+8) = 16
x+√x√(x+8) = 4
Factorize:
√x*(√x+√(x+8)) = 4
Replacing:
√x * 4 = 4
=> x=1

copernic

Got x=1 as the only solution after just guessing and checking!

scottleung

In this case you can't introduce extraneous rolutions by squaring once but you might when you do it the 2nd time

septembrinol

sqrt(x+8)+sqrt(x)=4
sqrt(x+8)=4-sqrt(x)
x+8=16-8sqrt(x)+x
8=16-8sqrt(x)
-8=-8sqrt(x)
sqrt(x)=1
x=1
Plugging x=1 into the equation, we see that it satisfies the equality. To prove that this is the only solution, the functions of the LHS and RHS must intersect only once. y=4 is a horizontal, constant line, so we need to prove that sqrt(x+8)+sqrt(x) doesn't change direction (monotonic), or in other words STRICTLY decreases or STRICTLY increases. We note that as x increases, the square roots get larger, hence making the function value larger. So it strictly increases. Therefore x=1 is the only solution.

kobalt

Let √(x+8) = a and √(x) = b
Then a + b = 4 and a² - b² = 8 2(a + b) = 8 and a² - b² = 8
a² - b² = 2(a + b) —> a - b = 2
a - b = 2 and a + b = 4 —>
2a = 6 —> a = 3 therefore
b = 1
The rest is substitutions and calculations.

solitude_taster

You said for the 2nd method it only works for certain scenarios, so, when the case is not these scenarios, does it mean it results in wrong answer or doesn't result with an answer?

williamsomerset

I would never use method 1a) because it is no good idea to keep both roots on the same side. Always distribute the roots as evenly as possible to both sides, in case of two roots, one on each side. This minimizes squaring operations.

goldfing