filmov
tv
Find the area of the quadrilateral
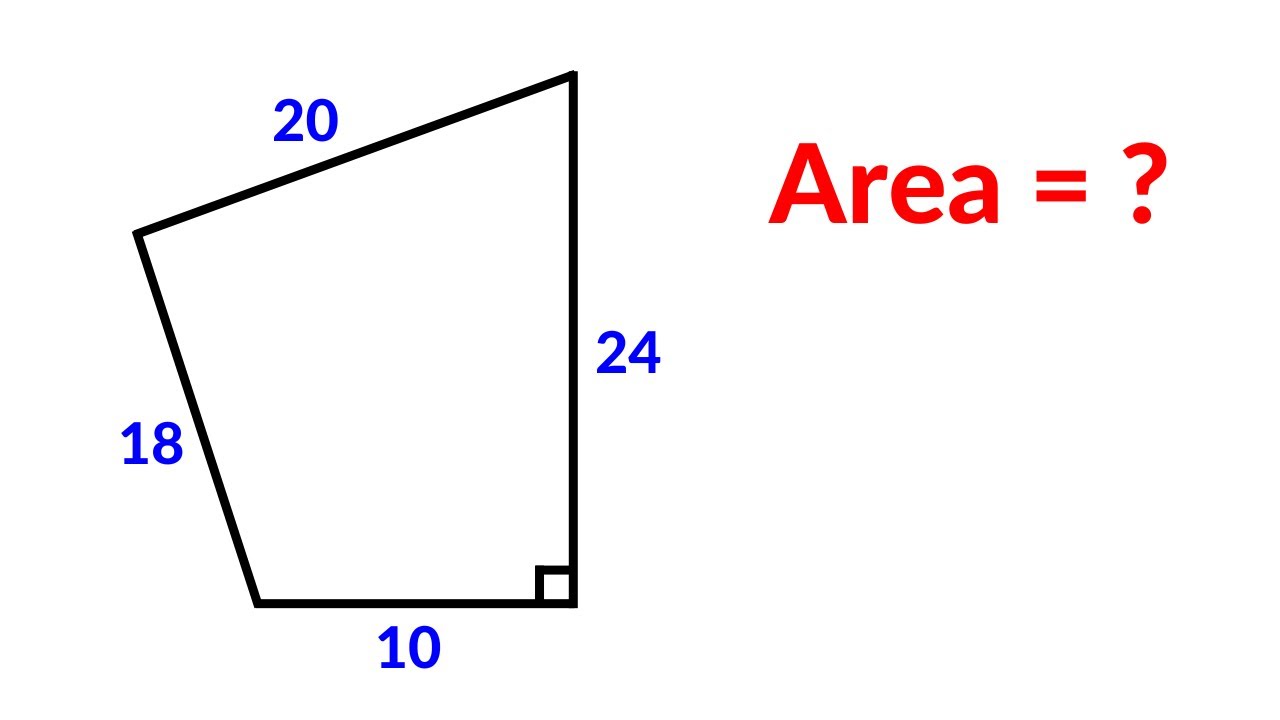
Показать описание
How to find the area of a quadrilateral
GET MY EBOOKS
•••••••••••••••••••••••
OTHER CHAPTERS : COMING SOON.....
--------------------------------------------------------------------------------
Join the channel to become a member
GET MY EBOOKS
•••••••••••••••••••••••
OTHER CHAPTERS : COMING SOON.....
--------------------------------------------------------------------------------
Join the channel to become a member
Math Antics - Area
Find the Area Challenge
How to Find the Area of a Rectangle | Math with Mr. J
Area of a Rectangle, Triangle, Circle & Sector, Trapezoid, Square, Parallelogram, Rhombus, Geome...
Finding the Area of a Composite Figure | Area of Composite Rectangles
How to Find Area | Rectangles, Squares, Triangles, & Circles | Math Mr. J
Area for Kids
Area of square | How to find area of the square #shorts
How to Find the Area of Triangles, Trapeziums & Parallelograms
Can you find area of the Green shaded Triangle? | (Quadrilateral) | #math #maths | #geometry
Find the area of the quadrilateral
How to Find the Area of a Square | Math with Mr. J
Area and Perimeter
How To Find The Area of a Rectangle | Math
Find the area of the rectangle | A Very Nice Geometry Problem | Math Olympiad
Find the Blue Area
How to Find the Area of Rectangles and Squares | Math with Mr. J
How to Find the Surface Area of a Rectangular Prism | Math with Mr. J
How to Find the Area of a Triangle | Calculate the Area of a Triangle
Area of rectangle | How to find area of a rectangle #shorts
Easy Way To Find The Area Of A Circle! #Shorts
Area of Parallelograms | How to Find the Area of a Parallelogram
How to Find the Area of the Shaded Region | Square in a Square | Math with Mr. J
How to Find the Area of a Circle | Area of a Circle Step by Step
Комментарии
 0:10:26
0:10:26
 0:04:33
0:04:33
 0:04:43
0:04:43
 0:20:35
0:20:35
 0:07:14
0:07:14
 0:22:10
0:22:10
 0:08:58
0:08:58
 0:00:30
0:00:30
 0:09:11
0:09:11
 0:08:26
0:08:26
 0:09:52
0:09:52
 0:02:48
0:02:48
 0:17:49
0:17:49
 0:11:38
0:11:38
 0:09:24
0:09:24
 0:02:41
0:02:41
 0:06:57
0:06:57
 0:04:57
0:04:57
 0:06:37
0:06:37
 0:00:30
0:00:30
 0:00:30
0:00:30
 0:04:30
0:04:30
 0:03:32
0:03:32
 0:06:39
0:06:39