Geometrically Defining the Cross Product | Multivariable Calculus

TYPO: The formula at 3:55 for algebraically computing the determinant has a typo. It is a NEGATIVE in front of the j hat term, not a positive.

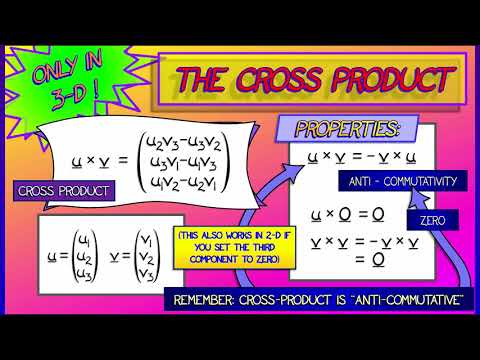
The cross product is a way to multiply two (three dimensional) vectors together and get a third vector as a result. However, in mathematics, we would only do this if it was useful. So in this video we begin with the purpose and work backwards to the computation. I describe the two geometric goals of the cross product:
1) Finding orthogonal vectors
2) Finding the area of a parallelogram
From these goals we define a geometric cross product. I also state how to compute it algebraically at the end.

****************************************************
YOUR TURN! Learning math requires more than just watching videos, so make sure you reflect, ask questions, and do lots of practice problems!
****************************************************

****************************************************
Other Course Playlists:

***************************************************

► Want to learn math effectively? Check out my "Learning Math" Series:

►Want some cool math? Check out my "Cool Math" Series:

*****************************************************

*****************************************************

*****************************************************

This video was created by Dr. Trefor Bazett

BECOME A MEMBER:

MATH BOOKS & MERCH I LOVE:

[chunlangong]

Clearly, simply, visually explained, you are an excellent educator

[markpadley]

These are first class videos and explanations - helping me greatly as I revisit topics after many years in the course of my post-graduate research - keep them coming Trefor!

[marcelojay]

Wow. The geometric explanation is crystal clear

[nexovec]

It's actually called the right-hand screw rule, and it's called that because it works exactly 50% of the time...

[sam]

There is no coincidence in math. To understand the connection between determinants structure for computing cross product is captured in 3blue1brown channel. Happy learning ❤️❤️

[chilli]

I wonder how other people claim to be good at mathematics and don't know the geometrical meanings 😂😂😂

Super OP explanation of cross product

[bishwajeetneupane]

This video was really aswome💖💖... It made me really easy to learn about cross product.

[sergiolucas]

Really good video, best channel for grasping the geometric significance of math stuff :)

[chilli]

I wish to become such a mathematician ❤

[Michallote]

Hey Dr. Trefor you should really cover Geometric Algebra (Clifford Algebra)!!!. The wedge product is so much more intuitive. I really feel the cross product is unintuitive and holds back a great portion of useful physics because it basically interprets something that should be a plane as a vector (instead of letting it be it's own thing in the form of a oriented plane, bivectors). And it is in my opinion holding back progress in physics education. The answer to it is to use instead the wedge or outer product, the geometric product and bivectors. Cheers I hope people really look this up if they are confused!!

[ericerpelding]

Can the "Right Hand Rule" be defined without using anthropomorphic aids?

[Limbaugh_]

I wish my physics teacher did this last semester

[sathyamoorthy]

thanks for this sir!!!! can you please upload some videos on matrix and determinants

[sushma.vallabhuni]

Please explain why every plane has normal line

[borissimovic]

Can someone please explain, if you can how the length of a vector, which is 1D “a line” (length of cross product vector) can be equal to the area which is 2D (2d space includes more information width and length) for example something has a length of 10cm not 10cm2, how can length be expressed in area terms aisnce length is 1D and area is 2D?

[DanijelAleksicMath]

What software do you use for these videos?

[mohammedshalabi]

Hi sir. I just want to ask a question. Why is the height equals to b×sin(angle) not b×a.In another way why is the area of parallelogram doesn't equal to a×b

[kalengray]

i thought cross product was (i - j + k)... now I'm confused...

[solcarzemog]

I came here for the JUSTIFICATION of the equivalence between the geometric and algebraic expressions... 😕😕