Geometric Intuition for the Computation of Dot Products, Cross Products, and Determinants #SoME3

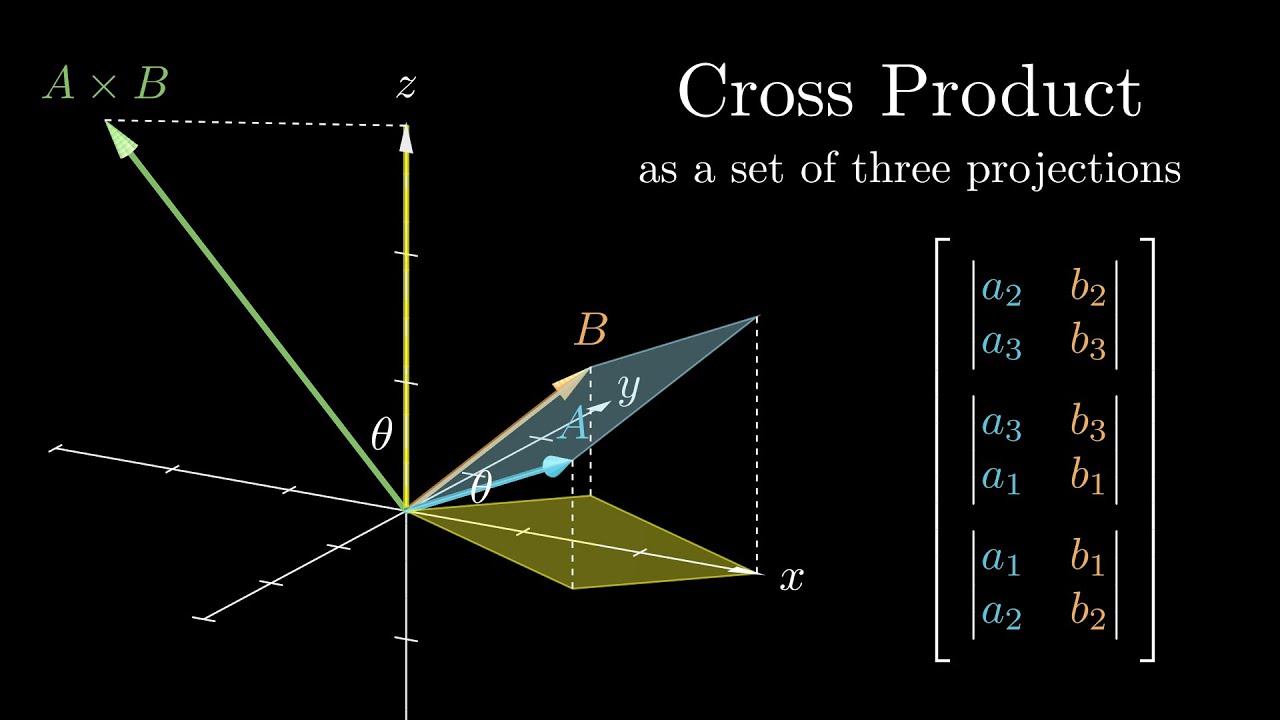
A look at the connection between the geometry of the dot product, cross product, and determinant, and their methods of computation.

0:00 Dot Product: law of cosines
2:03 Cross Product: projection to a plane
5:09 Determinant: permutation of elements

[kanhaiyalalrajput]

Very nice video with crystal clear explanation

[mndtr]

Not gonna lie that's one of the best videos about linear algebra I saw

[maix]

Great Video !
One remark I had while watching the video is that having the 3D plot constantly rotation was an issue for me, since I wanted to fully explore the details of the plot while you were speaking.
Since the plot was always rotating, it was very hard to actually be able to get those details (I know that the plot was representing a simple concept, but I like to be able to really get any last details about something like this. It might have been some sort of approximation of the distances and such. They weren't necessary to understand, but it might be for others)

otherwise the tone of the voice was awesome. You might want to give it a bit more life with more intonations, but I really enjoyed this video.

The topic was awesome too. I learned dot and cross product at school, but never really got any answer as to why they behaved like this.
The determinant of a matrix was also complete mystery for me. I always assumed it was a completely algebraic thing that someone found while trying to inverse matrices, but seeing that they have an actual geometrical reason + a "quick" formula to get any n-sized square matrices determinant was also great !

This video is very good and I wish you best of luck !
Please continue to find other "small" topics like this where you can make people eyes wide open :D

[kentkeatha]

great video! Too many books just rather let me memorise the formula instead of understand the derivation, u save my life.

[MathsSciencePhilosophy]

Coming back to this video after 1 year with my second account ❤

[borissimovic]

The confusing part is the projection of the second determinant a3*b1-b3*a1 it's not visually clear to me (that's the one in the middle of the 3 determinants). The relation between vector AXB and the axis where it is projected(this is the Y-axis) should be equivalent to the relationship between the AB plane and its projection(which is on the ZX plane) that is because the angles should be the same but I can't see that the angles are the same, what is the angle between AB plane and ZX-axis? Then the relation between the Y-Axis and ZX-plane should be equivalent to the relationship between Vector AXB and AB plane I think. Generally, I think this part should be better explained. Otherwise really great and useful video.

[shururururme]

Thats some very helpfull intuition but i still have a problem with it .

At minute 3:25 vector a and vector b are conviniently placed in such a way that they both have the same angle to the x/y plane. Needles to say, most of the time thats not the case.

So is there any other way to understand this intuition when the angles between the x/y plane and the a/b vectors differ ?

[martinsanchez-hwfi]

I still do not feel like I grasp the justification of extending the cosine to higher dimensions