filmov
tv
Area between curves; Both dx and dy Integration

Показать описание
We practice setting up the definite integrals required to find the area of the region bounded by two functions. We set up definite integrals with respect to both x and y. The functions are given to us as functions of x, y=x^2 and y = 2-x. In the first segment of the video, we rewrite the equations of the curves as functions of y which will allow us to integrate with respect to y. In the second segment of the video, we set up the dx definite integral that would give the area of the region, subtracting the top function minus the bottom. In the third segment of the video, we set up the dy definite integrals that would give the area of the region, subtracting the right function minus the left. In each case, we discuss the orientation of the representative rectangle. We do not evaluate the integrals.
Finding the Area Between Two Curves by Integration
Area between curves; Both dx and dy Integration
Area between curves | Applications of definite integrals | AP Calculus AB | Khan Academy
Choosing 'dx' or 'dy' for Area Two Between Curves (Calculus)
Area between curves with multiple boundaries
Area between curves
Area between curves - dx (KristaKingMath)
Find the area enclosed by the two curves
Area between Curves dx
AP CALC - Areas between curves dx HW
AP CALC - Areas between curves dx
Unit 10 Lecture 1 - Areas between Curves dx
6.1 Areas Between Curves | Video 2 - Area Using dx Integral || Calculus 1
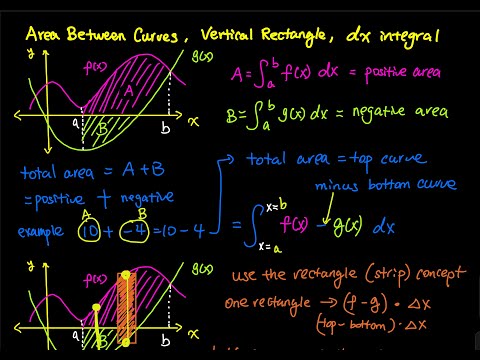
6.1 Part 1/6: Concepts of Area Between Curves, Vertical Rectangle, dx Integral | Integral Calculus
6.1 Part 4/6: More Challenging Area Between Curves, Vertical Rectangle, dx Integral | Integral Calc
AP Calculus Area with dx #shorts #integral #apcalculus
Integration 23 Area Between Curves Deciding Between dx and dy
Area between a curve and the x-axis: negative area | AP Calculus AB | Khan Academy
7-2 Area Between Two Curves (dx and dy)
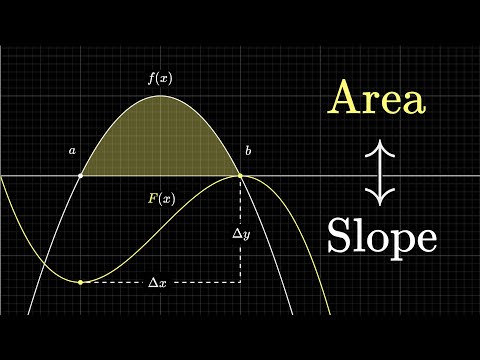
What does area have to do with slope? | Chapter 9, Essence of calculus
7.1.3 Finding The Area Enclosed By The Given Curves “dx” (must split up integral to get area)
Finding the Area Under a Curve using Definite Integration
Why do integrals always have a dx?
Ex 1: Area Bounded by Two Functions
Комментарии
 0:07:52
0:07:52
 0:05:54
0:05:54
 0:06:50
0:06:50
 0:10:46
0:10:46
 0:06:54
0:06:54
 0:04:09
0:04:09
 0:10:29
0:10:29
 0:07:09
0:07:09
 0:10:43
0:10:43
 0:53:35
0:53:35
 0:55:59
0:55:59
 1:05:42
1:05:42
 0:08:55
0:08:55
 0:14:08
0:14:08
 0:16:24
0:16:24
 0:00:47
0:00:47
 0:31:45
0:31:45
 0:07:28
0:07:28
 1:07:11
1:07:11
 0:12:39
0:12:39
 0:27:05
0:27:05
 0:17:14
0:17:14
 0:04:37
0:04:37
 0:04:40
0:04:40